Trung Tâm Luyện Thi Đại Học
Thể tích khối chóp - Một mặt bên vuông góc với đáy
Dạng 2. Một mặt bên vuông góc với đáy - Phần 1
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa SC và mặt phẳng đáy bằng 45O. Thể tích khối chóp S.ABCD bằng:
A. \( \frac{{{a}^{3}}\sqrt{3}}{12} \)
B. \( \frac{{{a}^{3}}\sqrt{3}}{9} \)
C. \( \frac{{{a}^{3}}\sqrt{5}}{24} \)
D. \( \frac{{{a}^{3}}\sqrt{5}}{6 }\)
Hướng dẫn giải:
Đáp án D.

Gọi H là trung điểm của AB, \( \Delta SAB \) cân tại S \( \Rightarrow SH\bot AB \)
\( \left. \begin{align} & (SAB)\bot (ABCD) \\ & (SAB)\cap (ABCD)=AB \\ & SH\subset (SAB);SH\bot AB \\ \end{align} \right\}\Rightarrow SH\bot (ABCD) \)
\( \widehat{\left( SC,(ABCD) \right)}=\widehat{SCH}={{45}^{0}} \) \( \Rightarrow \Delta SHC \) vuông cân tại H.
\( \Rightarrow SH=HC=\sqrt{B{{C}^{2}}+B{{H}^{2}}}=\sqrt{{{a}^{2}}+\frac{1}{4}{{a}^{2}}}=\frac{a\sqrt{5}}{2} \)
\( {{S}_{ABCD}}=A{{B}^{2}}={{a}^{2}} \)
\( \Rightarrow {{V}_{S.ABCD}}=\frac{1}{3}.{{S}_{ABCD}}.SH=\frac{1}{3}.{{a}^{2}}.\frac{a\sqrt{5}}{2}=\frac{{{a}^{3}}\sqrt{5}}{6} \)
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tam giác SAB là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng (SCD) tạo với đáy 30O. Thể tích khối chóp S.ABCD là
A. \( \frac{{{a}^{3}}\sqrt{3}}{4} \)
B. \( \frac{{{a}^{3}}\sqrt{3}}{2} \)
C. \( \frac{{{a}^{3}}\sqrt{3}}{36} \)
D. \( \frac{5{{a}^{3}}\sqrt{3}}{36} \)
Hướng dẫn giải:
Đáp án A.
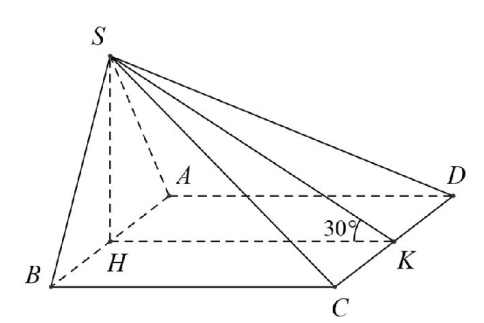
Gọi H, K lần lượt là trung điểm của AB, CD.
Suy ra: \( SH\bot (ABCD) \) và \( \widehat{\left( (SCD),(ABCD) \right)=}\widehat{SKH}={{30}^{0}} \).
Xét \( \Delta SHK \) vuông tại H, ta có: \( HK=\frac{SH}{\tan {{30}^{0}}}=\frac{\frac{\sqrt{3}}{2}a}{\frac{\sqrt{3}}{3}}=\frac{3a}{2} \).
Vậy \({{V}_{S.ABCD}}=\frac{1}{3}SH.{{S}_{ABCD}}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.a.\frac{3a}{2}=\frac{{{a}^{3}}\sqrt{3}}{4}\)
Câu 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC, AB = a, \( AC=a\sqrt{3} \), \( SB=a\sqrt{2} \). Thể tích của khối chóp S.ABC bằng
A. \( \frac{{{a}^{3}}\sqrt{3}}{2} \)
B. \( \frac{{{a}^{3}}\sqrt{6}}{2} \)
C. \( \frac{{{a}^{3}}\sqrt{3}}{6} \)
D. \( \frac{{{a}^{3}}\sqrt{6}}{6} \)
Hướng dẫn giải:
Đáp án C.
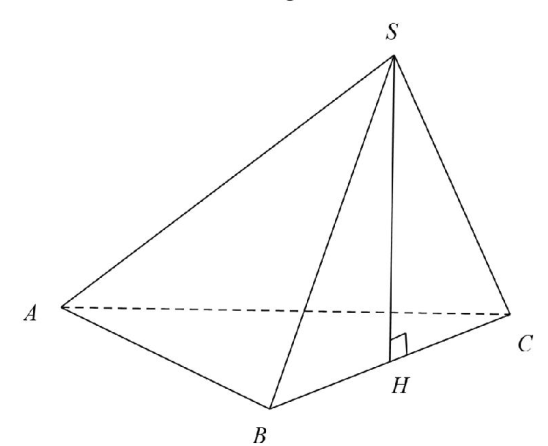
Xét tam giác ABC vuông tại A có: \( BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{{{a}^{2}}+{{\left( a\sqrt{3} \right)}^{2}}}=2a \)
H là trung điểm của BC nên BH = a.
Xét tam giác SBH vuông tại H có: \( SH=\sqrt{S{{B}^{2}}-H{{B}^{2}}}=\sqrt{{{\left( a\sqrt{2} \right)}^{2}}-{{a}^{2}}}=a \)
Diện tích đáy ABC là: \( {{S}_{ABC}}=\frac{1}{2}AB.AC=\frac{1}{2}{{a}^{2}}\sqrt{3} \)
Thể tích của khối chóp S.ABC là: \( V=\frac{1}{3}SH.{{S}_{\Delta ABC}}=\frac{1}{3}.a.\frac{1}{2}.{{a}^{2}}\sqrt{3}=\frac{{{a}^{3}}\sqrt{3}}{6} \)
Câu 4. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có AB = a, \( BC=a\sqrt{3} \). Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính a thể tích của khối chóp S.ABC.
A. \( V=\frac{{{a}^{3}}\sqrt{6}}{6} \)
B. \( V=\frac{{{a}^{3}}\sqrt{6}}{12} \)
C. \( V=\frac{2{{a}^{3}}\sqrt{6}}{3} \)
D. \( V=\frac{{{a}^{3}}\sqrt{6}}{4} \)
Hướng dẫn giải:
Đáp án B.
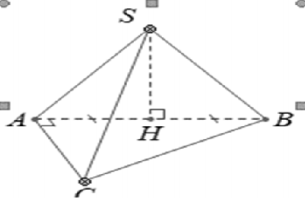
Gọi H là trung điểm của cạnh AB.
Do \( \Delta SAB \) đều nên \( SH\bot AB \)
\( \left. \begin{align} & (SAB)\bot (ABC) \\ & (SAB)\cap (ABC)=AB \\ & SH\subset (SAB),SH\bot AB \\ \end{align} \right\}\Rightarrow SH\bot (ABC) \)
Vậy SH là chiều cao của khối chóp S.ABC.
\( \Delta ABC \) vuông tại A, ta có: \( AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}-{{a}^{2}}}=a\sqrt{2} \)
\( {{S}_{\Delta ABC}}=\frac{1}{2}AB.AC=\frac{1}{2}.a.a\sqrt{2}=\frac{{{a}^{2}}\sqrt{2}}{2}\), \( SH=\frac{a\sqrt{3}}{2} \) .
Thể tích khối chóp S.ABC là: \( {{V}_{S.ABC}}=\frac{1}{3}{{S}_{ABC}}.SH=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{2}}{2}.\frac{a\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{6}}{12} \)
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A và có AB = a, \( BC=a\sqrt{3} \). Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC). Tính theo a thể tích của khối chóp S.ABC.
A. \(V=\frac{{{a}^{3}}\sqrt{6}}{12}\)
B. \(V=\frac{{{a}^{3}}\sqrt{6}}{4}\)
C. \(V=\frac{{{a}^{3}}\sqrt{6}}{8}\)
D. \(V=\frac{{{a}^{3}}\sqrt{6}}{6}\)
Hướng dẫn giải:
Đáp án A.
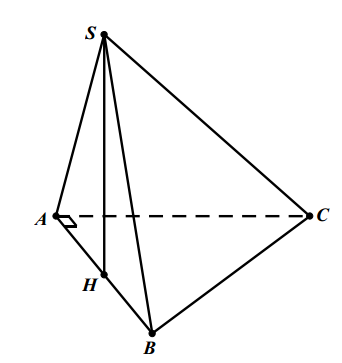
Xét tam giác ABC vuông tại A, ta có: \( AC=\sqrt{B{{C}^{2}}-A{{B}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}-{{a}^{2}}}=a\sqrt{2} \)
Diện tích tam giác ABC là: \( {{S}_{\Delta ABC}}=\frac{1}{2}.AB.AC=\frac{1}{2}.a.a\sqrt{2}=\frac{{{a}^{2}}\sqrt{2}}{2} \).
Gọi H là trung điểm AB thì \( SH\bot AB \).
Vì \( \left. \begin{align} & (SAB)\bot (ABC) \\ & (SAB)\cap (ABC)=AB \\ \end{align} \right\}\Rightarrow SH\bot (ABC) \)
Suy ra SH là chiều cao của khối chóp S.ABC.
Tam giác SAH vuông tại H nên \( SH=SA.\sin \widehat{SAH}=a.\sin {{60}^{0}}=\frac{a\sqrt{3}}{2} \).
Thể tích khối chóp S.ABC là \( V=\frac{1}{3}.{{S}_{\Delta ABC}}.SH=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{2}}{2}.\frac{a\sqrt{3}}{2}=\frac{{{a}^{3}}\sqrt{6}}{12} \).
Câu 6. Cho hình chóp S.ABC có đáy là tam giác cân tại A, AB = AC = a, \( \widehat{BAC}={{120}^{0}} \). Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.
A. \( V=\frac{{{a}^{3}}}{8} \)
B. \( V={{a}^{3}} \)
C. \( V=\frac{{{a}^{3}}}{2} \)
D. \( V=2{{a}^{3}} \)
Hướng dẫn giải:
Đáp án A.
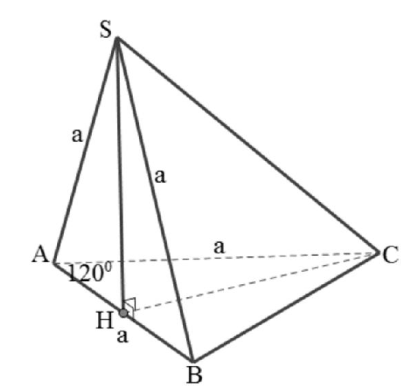
Gọi H là trung điểm đoạn AB \( \Rightarrow SH\bot AB \) (vì tam giác SAB là tam giác đều)
\(\left\{ \begin{align} & (SAB)\bot (ABC) \\ & (SAB)\cap (ABC)=AB \\ & SH\subset (SAB);SH\bot AB \\ \end{align} \right.\Rightarrow SH\bot (ABC)\)
Nhận thấy \( \Delta SAB \) là tam giác đều cạnh a \( \Rightarrow SH=\frac{a\sqrt{3}}{2} \).
\( {{S}_{\Delta ABC}}=\frac{1}{2}AB.AC.\sin {{120}^{0}}=\frac{{{a}^{2}}\sqrt{3}}{4} \)
Vậy thể tích khối chóp S.ABC là: \( {{V}_{S.ABC}}=\frac{1}{3}.SH.{{S}_{\Delta ABC}}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}}{8} \).
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD) là 30O. Thể tích của khối chóp S.ABCD là:
A. \( \frac{2{{a}^{3}}\sqrt{3}}{3} \)
B. \( \frac{{{a}^{3}}\sqrt{3}}{3} \)
C. \( \frac{4{{a}^{3}}\sqrt{3}}{3} \)
D. \( 2{{a}^{3}}\sqrt{3} \)
Hướng dẫn giải:
Đáp án D.
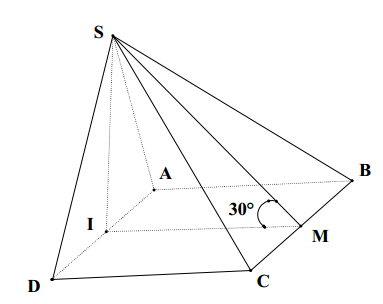
Trong tam giác đều SAD gọi I là trung điểm AD \( \Rightarrow SI\bot AD\Rightarrow SI\bot (ABCD) \).
Gọi M là trung điểm BC \( \Rightarrow BC\bot IM \) (1)
Mặt khác do \( SI\bot (ABCD)\Rightarrow BC\bot SI \) (2)
Từ (1), (2) suy ra \( BC\bot SM \).
Vậy góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD) chính là góc \( \widehat{SMI}={{30}^{0}} \).
Xét tam giác vuông SIM có \( IM=\frac{SI}{\tan {{30}^{0}}}=3a \) (ví tam giác SAD là tam giác đều cạnh 2a nên \( SI=a\sqrt{3} \))
Vậy thể tích của khối chóp S.ABCD là \( V=\frac{1}{3}.{{S}_{ABCD}}.SI=\frac{1}{3}AD.BC.SI=2{{a}^{3}}\sqrt{3} \)
Câu 8. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), \( \widehat{SAB}={{30}^{0}} \), SA = 2a. Tính thể tích V của khối chóp S.ABCD.
A. \( V=\frac{{{a}^{3}}\sqrt{3}}{6} \)
B. \( V={{a}^{3}} \)
C. \( V=\frac{{{a}^{3}}}{9} \)
D. \( V=\frac{{{a}^{3}}}{3} \)
Hướng dẫn giải:
Đáp án D.
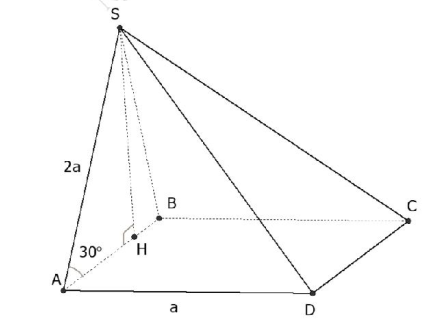
Gọi H là hình chiếu vuông góc của S lên cạnh AB.
Do \( \left. \begin{align} & (SAB)\bot (ABCD) \\ & (SAB)\cap (ABCD)=AB \\ \end{align} \right\}\Rightarrow SH\bot (ABCD) \)
Xét tam giác SAH vuông tại H, ta có: \(\sin \widehat{SAB}=\frac{SH}{SA}\)\(\Rightarrow SH=SA.\sin {{30}^{0}}=a\).
Mặt khác: \( {{S}_{ABCD}}=A{{D}^{2}}={{a}^{2}} \)
Nên \( {{V}_{S.ABCD}}=\frac{1}{3}.{{S}_{ABCD}}.a=\frac{1}{3}.{{a}^{2}}.a=\frac{{{a}^{3}}}{3} \)
Câu 9. (Đề Minh Họa – 2017) Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng \( a\sqrt{2} \). Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng \( \frac{4}{3}{{a}^{3}} \). Tính khoảng cách h từ B đến mặt phẳng (SCD).
A. \( h=\frac{4}{3}a \)
B. \( h=\frac{3}{2}a \)
C. \( h=\frac{2\sqrt{5}}{5}a \)
D. \( h=\frac{\sqrt{6}}{3}a \)
Hướng dẫn giải:
Đáp án A.
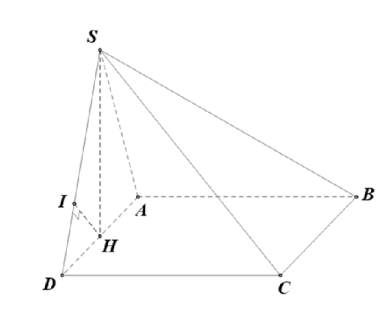
Gọi H là trung điểm của AD. Nên \( SH\bot AD \)
\( \left\{ \begin{align} & (SAD)\bot (ABCD) \\ & (SAD)\cap (ABCD)=AD \\ & AD\bot SH \\ \end{align} \right.\Rightarrow SH\bot (ABCD) \)
Ta có: \( {{S}_{ABCD}}=2{{a}^{2}} \)
\( \Rightarrow SH=\frac{3V}{{{S}_{ABCD}}}=\frac{3.\frac{4{{a}^{3}}}{3}}{2{{a}^{2}}}=2a \)
Gọi I là hình chiếu của H lên SD
\({{d}_{\left( B,(SCD) \right)}}={{d}_{\left( A,(SCD) \right)}}=2{{d}_{\left( H,(SCD) \right)}}=2IH\)
Mà \( IH=\frac{SH.HD}{SD}=\frac{SH.HD}{\sqrt{S{{H}^{2}}+H{{D}^{2}}}}=\frac{2a.\frac{a\sqrt{2}}{2}}{\sqrt{{{\left( 2a \right)}^{2}}+{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}}}=\frac{2}{3}a \)
Vậy \( {{d}_{\left( B,(SCD) \right)}}=\frac{4}{3}a \).
Câu 10. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và tam giác SAB đều nằm trong mặt phẳng vuông góc với đáy. Biết khoảng cách giữa hai đường thẳng SA và BD bằng \( \sqrt{21} \). Hãy cho biết cạnh đáy bằng bao nhiêu?
A. \( \sqrt{21} \)
B. 21
C. \( 7\sqrt{3} \)
D. 7
Hướng dẫn giải:
Đáp án D.
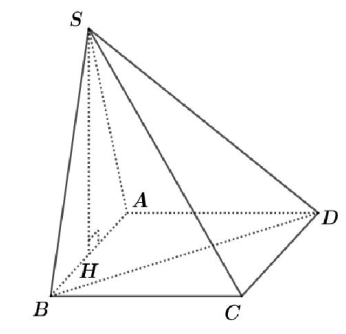
Giả sử AB = a. Gọi H là trung điểm của AB \( \Rightarrow SH\bot AB\Rightarrow SH\bot (ABCD) \)
Ta có:
\( \overrightarrow{SA}.\overrightarrow{BD}=\left( \overrightarrow{SH}+\overrightarrow{HA} \right).\left( \overrightarrow{BA}+\overrightarrow{BC} \right)=\overrightarrow{HA}.\overrightarrow{BA}=\frac{1}{2}{{a}^{2}} \)
\( \Leftrightarrow {{a}^{2}}\sqrt{2}\cos \left( \overrightarrow{SA},\overrightarrow{BD} \right)=\frac{1}{2}{{a}^{2}} \) \( \Leftrightarrow \cos \left( \overrightarrow{SA},\overrightarrow{BD} \right)=\frac{1}{2\sqrt{2}}\Rightarrow \sin \left( SA,BD \right)=\sqrt{\frac{7}{8}} \)
\( {{V}_{SABCD}}=\frac{1}{3}SH.AB.AD=\frac{1}{3}.\frac{a\sqrt{3}}{2}.{{a}^{2}}=\frac{\sqrt{3}}{6}{{a}^{3}}\Rightarrow {{V}_{SABD}}=\frac{\sqrt{3}}{12}{{a}^{3}} \).
\( \Leftrightarrow \frac{1}{6}SA.BD.{{d}_{\left( SA,BD \right)}}.\sin \left( SA,BD \right)=\frac{\sqrt{3}}{12}{{a}^{3}} \) \( \Leftrightarrow \frac{1}{6}a.a\sqrt{2}.\sqrt{21}.\sqrt{\frac{7}{8}}=\frac{\sqrt{3}}{12}{{a}^{3}}\Leftrightarrow a=7 \)
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









