Trung Tâm Luyện Thi Đại Học
Thể tích khối chóp - Khối chóp đều
Dạng 3. Khối chóp đều
Câu 1. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng 60O. Thể tích V của khối chóp S.ABCD bằng
A. \( V=\frac{{{a}^{3}}\sqrt{3}}{2} \)
B. \( V=\frac{{{a}^{3}}\sqrt{2}}{2} \)
C. \( V=\frac{{{a}^{3}}\sqrt{3}}{6} \)
D. \( V=\frac{{{a}^{3}}\sqrt{2}}{6} \)
Hướng dẫn giải:
Đáp án C.
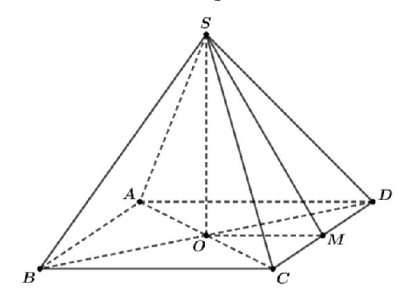
Gọi O là tâm của đáy, gọi M là trung điểm của BC.
Ta có: \( \left\{ \begin{align} & SO\bot BC \\ & OM\bot BC \\ \end{align} \right.\Rightarrow (SOM)\bot BC \)
Suy ra: \( \widehat{\left( (SCD),(ABCD) \right)}=\widehat{\left( SM,OM \right)}=\widehat{SMO}={{60}^{0}} \).
Có \(OM=\frac{1}{2}BC=\frac{1}{2}a\), \(SO=OM\tan {{60}^{0}}=\frac{a\sqrt{3}}{2}\).
Thể tích khối chóp S.ABCD là: \( {{V}_{S.ABCD}}=\frac{1}{3}SO.{{S}_{ABCD}}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.{{a}^{2}}=\frac{{{a}^{3}}\sqrt{3}}{6} \).
Câu 2. Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 45O. Thể tích khối chóp S.ABCD là
A. \( \frac{{{a}^{3}}}{3} \)
B. \( \frac{{{a}^{3}}\sqrt{2}}{6} \)
C. \( \frac{{{a}^{3}}}{6} \)
D. \( \frac{{{a}^{3}}\sqrt{2}}{3} \)
Hướng dẫn giải:
Đáp án B.
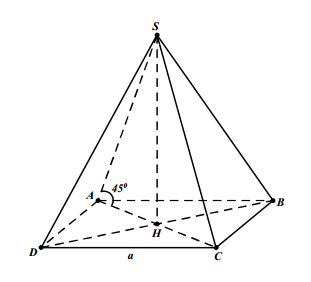
Vì S.ABCD là hình chóp đều nên đáy ABCD là hình vuông và chân đường cao H trùng với tâm của hình vuông ABCD.
Diện tích đáy của hợp chất S.ABCD là \( {{S}_{ABCD}}={{a}^{2}} \).
Nhận thấy HA là hình chiếu vuông góc của SA trên (ABC).
Vì thế \( \widehat{\left( SA,(ABC) \right)}=\widehat{\left( SA,HA \right)}=\widehat{SAH}={{45}^{0}} \)
Xét tam giác ABC vuông tại B, ta có: \( AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=a\sqrt{2} \). Suy ra \( HA=\frac{a\sqrt{2}}{2} \)
Tam giác SHA vuông tại H và có \( \widehat{SAH}={{45}^{0}} \) nên là tam giác vuông cân tại H. Suy ra \( SH=HA=\frac{a\sqrt{2}}{2} \).
Thể tích khối chóp S.ABCD là \( V=\frac{1}{3}.{{S}_{ABCD}}.SH=\frac{1}{3}.{{a}^{2}}.\frac{a\sqrt{2}}{2}=\frac{{{a}^{3}}\sqrt{2}}{6} \).
Câu 3. Có một hình chóp tứ giác đều có cạnh đáy bằng 2a và cạnh bên tạo với mặt phẳng đáy một góc 45O. Thể tích của khối chóp đó là
A. \( \frac{4{{a}^{3}}\sqrt{2}}{3} \)
B. \( \frac{{{a}^{3}}\sqrt{2}}{8} \)
C. \( \frac{{{a}^{3}}\sqrt{2}}{6} \)
D. \( 2\sqrt{2}{{a}^{3}} \)
Hướng dẫn giải:
Đáp án A.

Dựng hình chóp tứ giác đều S.ABCD thỏa mãn các điều kiện đề bài với O = AC \( \cap \) BD.
Theo giả thiết ta có: AB = 2a, SA tạo với mặt phẳng (ABCD) một góc 45O suy ra \( \widehat{SAO}={{45}^{0}} \)
ABCD là hình vuông cạnh 2a nên tính được \( AC=2\sqrt{2}a\Rightarrow OA=a\sqrt{2} \)
Tam giác SOA vuông cân tại O vì có SO \( \bot \) OA, \( \widehat{SAO}={{45}^{0}} \) suy ra \( SO=OA=a\sqrt{2} \).
Vậy thể tích khối chóp là \( V=\frac{1}{3}{{S}_{ABCD}}.SO=\frac{1}{3}.4{{a}^{2}}.a\sqrt{2} \)
Câu 4. Cho hình chóp tam giác đều S.ABC, cạnh AB = a và cạnh bên hợp với đáy một góc 45O. Thể tích V của khối chóp là
A. \( V=\frac{{{a}^{3}}}{12} \)
B. \( V=\frac{{{a}^{3}}}{6} \)
C. \( V=\frac{{{a}^{3}}}{3} \)
D. \( V=\frac{{{a}^{3}}}{4} \)
Hướng dẫn giải:
Đáp án A.
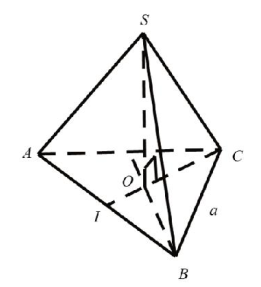
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì S.ABC là hình chóp tam giác đều nên SO \( \bot \) (ABC).
Do S.ABC là hình chóp tam giác đều nên các cạnh bên đều tạo với mặt đáy các góc bằng nhau.
Góc giữa cạnh SC với đáy là góc giữa hai đường thẳng SC và OC hay chính là góc \( \widehat{SCO} \).
Theo bài ra ta có: \( \widehat{SCO}={{45}^{0}} \Rightarrow \Delta SOC \) vuông cân tại O.
Tam giác ABC đều cạnh a nên \(CO=SO=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\).
Diện tích đáy là \({{S}_{\Delta ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}\).
Thể tích của khối chóp: \( V=\frac{1}{3}{{S}_{\Delta ABC}}.SO=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.\frac{a\sqrt{3}}{3}=\frac{{{a}^{3}}}{12} \)
Câu 5. Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng:
A. \( \frac{2{{a}^{3}}\sqrt{2}}{3} \)
B. \( \frac{8{{a}^{3}}}{3} \)
C. \( \frac{8{{a}^{3}}\sqrt{2}}{3} \)
D. \( \frac{4{{a}^{3}}\sqrt{2}}{3} \)
Hướng dẫn giải:
Đáp án D.
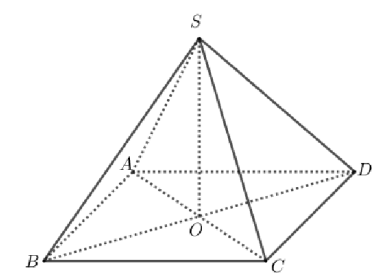
Gọi O là tâm của hình vuông ABCD, ta có: SO \( \bot \) (ABCD).
Xét tam giác SOA vuông tại O có SA = 2a, \( AO=\frac{1}{2}AC=\frac{1}{2}.2a\sqrt{2}=a\sqrt{2} \)
Suy ra: \( SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\sqrt{{{\left( 2a \right)}^{2}}-{{\left( a\sqrt{2} \right)}^{2}}}=a\sqrt{2} \)
Vậy \( {{V}_{S.ABCD}}=\frac{1}{3}.SO.{{S}_{ABCD}}=\frac{1}{3}.a\sqrt{2}.{{(2a)}^{2}}=\frac{4{{a}^{3}}\sqrt{2}}{3} \)
Câu 6. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tâm của đáy là O. Gọi M và N lần lượt là trung điểm của SA và BC. Biết góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng 60O. Tính thể tích khối chóp S.ABCD.
A. \( \frac{{{a}^{3}}\sqrt{10}}{6} \)
B. \( \frac{{{a}^{3}}\sqrt{30}}{2} \)
C. \( \frac{{{a}^{3}}\sqrt{30}}{6} \)
D. \( \frac{{{a}^{3}}\sqrt{10}}{3} \)
Hướng dẫn giải:
Đáp án C.
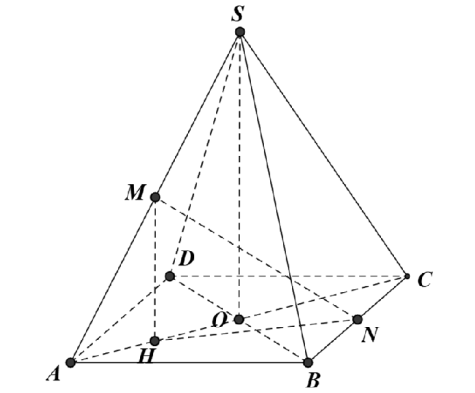
Gọi H là trung điểm AO. Khi đó góc giữa MN và (ABCD) là \( \widehat{MNH} \).
Ta có: \( HN=\sqrt{C{{N}^{2}}+C{{H}^{2}}-2CN.CH.\cos {{45}^{0}}}=\frac{a\sqrt{10}}{4} \)
Suy ra: \( MH=HN.\tan {{60}^{0}}=\frac{a\sqrt{10}}{4}.\sqrt{3}=\frac{a\sqrt{30}}{4} \)
Do đó: \( SO=2MH=\frac{a\sqrt{30}}{2} \)
\( {{V}_{S.ABCD}}=\frac{1}{3}.\frac{a\sqrt{30}}{2}.{{a}^{2}}=\frac{{{a}^{3}}\sqrt{30}}{6} \)
Câu 7. Nếu một hình chóp tứ giác đều có cạnh đáy bằng 2 và có diện tích xung quanh bằng \( 4\sqrt{3} \) thì có thể tích bằng
A. \(\frac{4\sqrt{2}}{3}\)
B. \(4\sqrt{3}\)
C. \(\frac{4\sqrt{3}}{3}\)
D. \(4\sqrt{2}\)
Hướng dẫn giải:
Đáp án A.
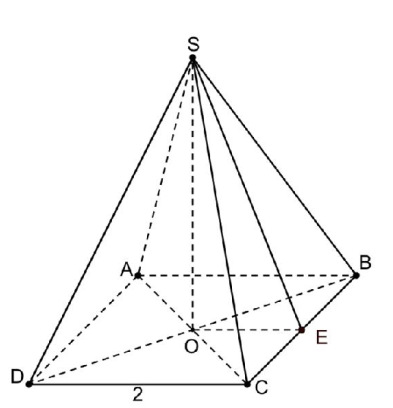
Xét hình chóp đều S.ABCD như hình vẽ
Kẻ \( OE\bot BC\Rightarrow \) E là trung điểm BC và BC \( \bot \) (SOE)
Do đó: \( BC\bot SE \)
Xét \(\Delta SOE\) vuông tại O, ta có:
\(S{{E}^{2}}=S{{O}^{2}}+O{{E}^{2}}\Rightarrow SE=\sqrt{S{{O}^{2}}+1}\)
Mặt khác: \( {{S}_{xq}}=4{{S}_{\Delta SBC}}\Leftrightarrow 4\sqrt{3}=4.\frac{1}{2}.SE.BC \)
\( \Leftrightarrow 4\sqrt{3}=2\sqrt{S{{O}^{2}}+1}.2\Leftrightarrow SO=\sqrt{2}\text{ }\left( x>0 \right) \)
\( {{V}_{S.ABCD}}=\frac{1}{3}.SO.{{S}_{ABCD}}=\frac{1}{3}.\sqrt{2}{{.2}^{2}}=\frac{4\sqrt{2}}{3} \)
Câu 8. Cho hình chóp đều S.ABC có SA = a. Gọi D, E lần lượt là trung điểm của SA, SC. Tính thể tích khối chóp S.ABC theo a, biết BD vuông góc với AE.
A. \(\frac{{{a}^{3}}\sqrt{21}}{54}\)
B. \(\frac{{{a}^{3}}\sqrt{3}}{12}\)
C. \(\frac{{{a}^{3}}\sqrt{7}}{27}\)
D. \(\frac{{{a}^{3}}\sqrt{21}}{27}\)
Hướng dẫn giải:
Đáp án A.
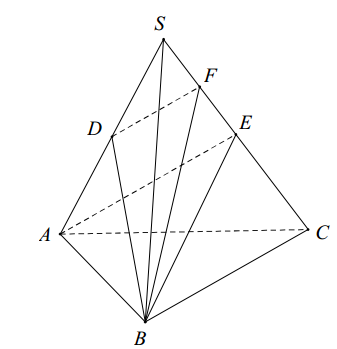
Gọi F là trung điểm SE \( \Rightarrow BD\bot DF \)
Gọi AB = x.
Ta có: \( B{{E}^{2}}=B{{D}^{2}}=A{{E}^{2}}=\frac{2A{{S}^{2}}+2A{{C}^{2}}-S{{C}^{2}}}{4}=\frac{2{{a}^{2}}+2{{x}^{2}}-{{a}^{2}}}{4}=\frac{{{a}^{2}}+2{{x}^{2}}}{4} \)
\( B{{F}^{2}}=\frac{2B{{S}^{2}}+2B{{E}^{2}}-S{{E}^{2}}}{4}=\frac{2{{a}^{2}}+\frac{{{a}^{2}}+2{{x}^{2}}}{2}-\frac{1}{4}{{a}^{2}}}{4}=\frac{9{{a}^{2}}+4{{x}^{2}}}{16} \)
\( B{{F}^{2}}=B{{D}^{2}}+D{{F}^{2}}\Leftrightarrow B{{F}^{2}}=\frac{5B{{D}^{2}}}{4}\Leftrightarrow \frac{9{{a}^{2}}+4{{x}^{2}}}{16}=\frac{5}{4}.\frac{{{a}^{2}}+2{{x}^{2}}}{4} \)
\( \Leftrightarrow 9{{a}^{2}}+4{{x}^{2}}=5{{a}^{2}}+10{{x}^{2}}\Leftrightarrow 4{{a}^{2}}=6{{x}^{2}}\Rightarrow x=a\sqrt{\frac{2}{3}} \)
Gọi H là hình chiếu của S lên (ABC) khi đó H là tâm đường tròn ngoại tiếp \( \Delta ABC \)
\( \Rightarrow SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{{{a}^{2}}-{{\left( \frac{2}{3}.\frac{x\sqrt{3}}{2} \right)}^{2}}}=\frac{a\sqrt{7}}{3} \)
Tam giác ABC đều có cạnh là \( x\Rightarrow {{S}_{\Delta ABC}}=\frac{{{x}^{2}}\sqrt{3}}{4}=\frac{{{a}^{2}}\sqrt{3}}{6} \)
Vậy \( {{V}_{S.ABC}}=\frac{1}{3}SH.{{S}_{\Delta ABC}}=\frac{1}{3}.\frac{a\sqrt{7}}{3}.\frac{{{a}^{2}}\sqrt{3}}{6}=\frac{{{a}^{3}}\sqrt{21}}{54} \)
Hoặc sử dụng công thức tính thể tích chóp tam giác ABC đều có cạnh bên bằng a, cạnh đáy bằng x.
\( {{V}_{S.ABC}}=\frac{{{x}^{2}}\sqrt{3{{a}^{2}}-{{x}^{2}}}}{12}=\frac{\frac{2{{a}^{2}}}{3}\sqrt{3{{a}^{2}}-\frac{2{{a}^{2}}}{3}}}{12}=\frac{{{a}^{3}}\sqrt{21}}{54} \)
Câu 9. Cho hình chóp tứ giác đều S.ABCD độ dài cạnh đáy là a. Biết rằng mặt phẳng (P) qua A và vuông góc với SC, cắt cạnh SB tại B’ với \( \frac{SB’}{SB}=\frac{2}{3} \). Tính thể tích của khối chóp S.ABCD
A. \( \frac{{{a}^{3}}\sqrt{6}}{6} \)
B. \( \frac{{{a}^{3}}\sqrt{6}}{4} \)
C. \( \frac{{{a}^{3}}\sqrt{6}}{2} \)
D. \( \frac{{{a}^{3}}\sqrt{6}}{3} \)
Hướng dẫn giải:
Đáp án A.
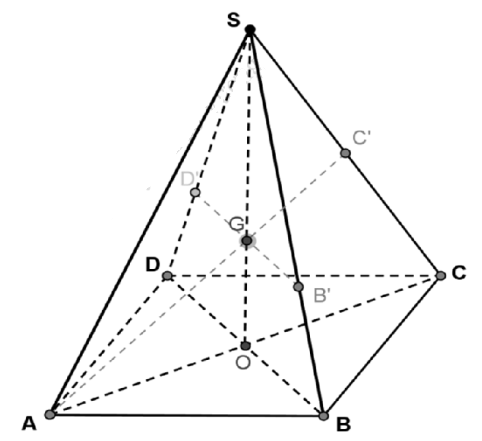
Ta có: \( \left. \begin{align} & BD\bot AC \\ & BD\bot SO \\ \end{align} \right\}\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot SC \)
Mà \( \left( P \right)\bot SC\Rightarrow \left( P \right)//BD \)
Trong (SAC), gọi \( G=A’C\cap SO\Rightarrow GB’//BD\Rightarrow \frac{SG}{SO}=\frac{SB’}{SB}=\frac{2}{3} \)
Suy ra G là trọng tâm \( \Delta SAC \Rightarrow C’ \) là trung điểm SC.
Nên \( \Delta SAC \) là tam giác đều cạnh \( AC=a\sqrt{2}\Rightarrow SO=a\sqrt{2}.\frac{\sqrt{3}}{2}=\frac{a\sqrt{6}}{2} \)
\( \Rightarrow {{V}_{S.ABCD}}=\frac{1}{3}{{S}_{ABCD}}.SO=\frac{1}{3}{{a}^{2}}.\frac{a\sqrt{6}}{2}=\frac{{{a}^{3}}\sqrt{6}}{6} \)
Câu 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng \( 2a\sqrt{3} \), khoảng cách giữa hai đường thẳng SA và CD bằng 3a. Thể tích khối chóp đã cho bằng:
A. \( {{a}^{3}}\sqrt{3} \)
B. \( 6\sqrt{3}{{a}^{3}} \)
C. \( 12{{a}^{3}} \)
D. \( \frac{8{{a}^{3}}\sqrt{3}}{3} \)
Hướng dẫn giải:
Đáp án C.
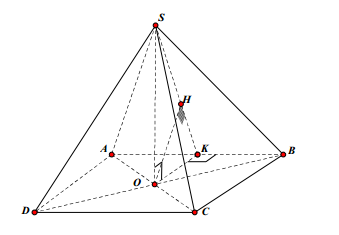
Gọi \( O=AC\cap BD \)
Ta có: \( \left\{ \begin{align} & CD//AB \\ & AB\subset (SAB) \\ \end{align} \right.\Rightarrow {{d}_{\left( CD,SA \right)}}={{d}_{\left( CD,(SAB) \right)}}={{d}_{\left( D,(SAB) \right)}}=2{{d}_{\left( O,(SAB) \right)}} \)
Kẻ \( \left\{ \begin{align} & OK\bot AB \\ & OH\bot SK \\ \end{align} \right.\Rightarrow OH\bot (SAB) \) \( \Rightarrow OH={{d}_{\left( O,(SAB) \right)}}=\frac{3a}{2} \)
Xét \( \Delta SOK: \frac{1}{O{{H}^{2}}}=\frac{1}{S{{O}^{2}}}+\frac{1}{O{{K}^{2}}}\Leftrightarrow SO=3a \)
Vậy thể tích khối chóp S.ABCD: \( V=\frac{1}{3}{{S}_{ABCD}}.SO=12{{a}^{3}} \)
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









