Trung Tâm Luyện Thi Đại Học
Phương trình bậc hai với các hàm số lượng giác - Phần 3
B. Bài tập có hướng dẫn giải (tiếp theo)
Câu 21. (KA – 2003) Giải phương trình: \( \cot x-1=\frac{\cos 2x}{1+\tan x}+{{\sin }^{2}}x-\frac{1}{2}\sin 2x \) (*)
Hướng dẫn giải:
Điều kiện: \( \left\{ \begin{align} & \sin 2x\ne 0 \\ & \tan x\ne -1 \\ \end{align} \right. \).
Đặt \( t=\tan x \) thì (*) thành:
\( \frac{1}{t}-1=\frac{\frac{1-{{t}^{2}}}{1+{{t}^{2}}}}{1+t}+\frac{1}{2}\left[ 1-\frac{1-{{t}^{2}}}{1+{{t}^{2}}} \right]-\frac{1}{2}.\frac{2t}{1+{{t}^{2}}} \)
\( \Leftrightarrow \frac{1-t}{t}=\frac{1-t}{1+{{t}^{2}}}+\frac{1}{2}.\frac{2{{t}^{2}}}{1+{{t}^{2}}}-\frac{t}{1+{{t}^{2}}}\text{ }(do\text{ }t\ne -1) \)
\( \Leftrightarrow \frac{1-t}{t}=\frac{{{t}^{2}}-2t+1}{1+{{t}^{2}}}=\frac{{{(1-t)}^{2}}}{1+{{t}^{2}}}\Leftrightarrow (1-t)(1+{{t}^{2}})={{(1-t)}^{2}}t \)
\( \Leftrightarrow \left[ \begin{align} & 1-t=0 \\ & 1+{{t}^{2}}=(1-t)t \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & t=1\text{ }(n) \\ & 2{{t}^{2}}-t+1=0\text{ }(\text{vô nghiệm}) \\ \end{align} \right. \) .
Vậy (*) \( \Leftrightarrow \tan x=1\Leftrightarrow x=\frac{\pi }{4}+k\pi \text{ }(\text{nhận }do\text{ }\sin 2x=1\ne 0) \).
Câu 22. Giải phương trình: \( \sin 2x+2\tan x=3 \) (*)
Hướng dẫn giải:
Điều kiện: \( \cos x\ne 0 \).
Đặt \( t=\tan x \) thì (*) thành:
\( \frac{2t}{1+{{t}^{2}}}+2t=3\Leftrightarrow 2t+(2t-3)(1+{{t}^{2}})=0\Leftrightarrow 2{{t}^{3}}-3{{t}^{2}}+4t-3=0 \)
\( \Leftrightarrow (t-1)(2{{t}^{2}}-t+3)=0\Leftrightarrow \left[ \begin{align}& t=1 \\ & 2{{t}^{2}}-t+3=0\text{ }(\text{vô nghiệm}) \\ \end{align} \right. \)
\( \Rightarrow \tan x=1\Leftrightarrow x=\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Câu 23. Giải phương trình: \( \cot x-\tan x+4\sin 2x=\frac{2}{\sin 2x} \) (*)
Hướng dẫn giải:
Điều kiện: \( \sin 2x\ne 0 \)
Đặt \( t=\tan x \) thì: \( \sin 2x=\frac{2t}{1+{{t}^{2}}} \) do \( \sin 2x\ne 0 \) nên \( t\ne 0 \).
(*) thành: \( \frac{1}{t}-t+\frac{8t}{1+{{t}^{2}}}=\frac{1+{{t}^{2}}}{t}=\frac{1}{t}+t\Leftrightarrow \frac{8t}{1+{{t}^{2}}}=2t \)
\( \Leftrightarrow \frac{8t}{1+{{t}^{2}}}=2t\Leftrightarrow \frac{4}{1+{{t}^{2}}}=1\text{ }(do\text{ }t\ne 0) \)
\( \Leftrightarrow {{t}^{2}}=3\Leftrightarrow t=\pm \sqrt{3}\text{ }(\text{nhận }do\text{ }t\ne 0) \)
\( \Rightarrow \tan x=\pm \sqrt{3}=\tan \left( \pm \frac{\pi }{3} \right)\Leftrightarrow x=\pm \frac{\pi }{3}+k\pi ,\text{ }k\in \mathbb{Z} \).
Câu 24. Giải phương trình: \( (1-\tan x)(1+\sin 2x)=1+\tan x \) (*)
Hướng dẫn giải:
Điều kiện: \( \cos x\ne 0 \).
Đặt \( t=\tan x \) thì (*) thành:
\( (1-t)\left( 1+\frac{2t}{1+{{t}^{2}}} \right)=1+t\Leftrightarrow (1-t)\frac{{{(t+1)}^{2}}}{1+{{t}^{2}}}=1+t \)
\( \Leftrightarrow (1+t)\left[ \frac{(1-t)(1+t)}{1+{{t}^{2}}}-1 \right]=0\Leftrightarrow \left[ \begin{align} & t=-1 \\ & \frac{(1-t)(1+t)}{1+{{t}^{2}}}=1 \\ \end{align} \right. \)
\( \Leftrightarrow \left[ \begin{align} & t=-1 \\ & 1-{{t}^{2}}=1+{{t}^{2}} \\ \end{align} \right.\Leftrightarrow t=-1\vee t=0 \).
Do đó: \( \left[ \begin{align} & \tan x=-1 \\ & \tan x=0 \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=-\frac{\pi }{4}+k\pi \\ & x=k\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
Câu 25. Cho phương trình: \( \cos 2x-(2m+1)\cos x+m+1=0 \) (*)
a) Giải phương trình khi \( m=\frac{3}{2} \).
b) Tìm m để (*) có nghiệm trên \( \left( \frac{\pi }{2};\frac{3\pi }{2} \right) \).
Hướng dẫn giải:
Ta có: (*) \( \Leftrightarrow 2{{\cos }^{2}}x-(2m+1)\cos x+m=0 \)
Đặt \( t=\cos x \) (điều kiện: \( \left| t \right|\le 1 \)).
Khi đó, phương trình trở thành: \( 2{{t}^{2}}-(2m+1)t+m=0 \)
\( \Leftrightarrow (2t-1)(t-m)=0\Leftrightarrow \left[ \begin{align} & t=\frac{1}{2} \\ & t=m \\ \end{align} \right. \).
a) Khi \( m=\frac{3}{2} \), phương trình thành: \( \left[ \begin{align} & \cos x=\frac{1}{2}\text{ }(n) \\ & \cos x=\frac{3}{2}\text{ }(\ell ) \\ \end{align} \right. \).
\( \Leftrightarrow x=\pm \frac{\pi }{3}+k2\pi ,\text{ }k\in \mathbb{Z} \).
b) Khi \( x\in \left( \frac{\pi }{2};\frac{3\pi }{2} \right) \) thì \( \cos x=t\in [-1;0) \).
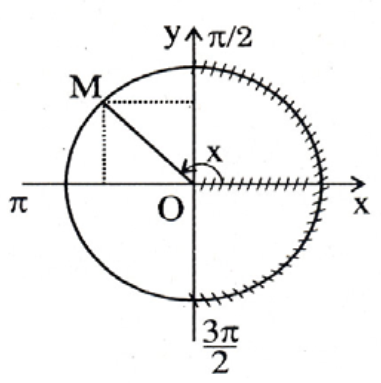
Do \( t=\frac{1}{2}\notin [-1;0] \) nên (*) có nghiệm trên \( \left( \frac{\pi }{2};\frac{3\pi }{2} \right) \) \( \Leftrightarrow m\in [-1;0) \)
Câu 26. Cho phương trình: \( (\cos x+1)(\cos 2x-m\cos x)=m{{\sin }^{2}}x \) (*)
a) Giải (*) khi \( m=-2 \).
b) Tìm m sao cho (*) có đúng hai nghiệm trên \( \left[ 0;\frac{2\pi }{3} \right] \).
Hướng dẫn giải:
Lời giải:
Ta có: (*) \( \Leftrightarrow (\cos x+1)(2{{\cos }^{2}}x-1-m\cos x)=m(1-{{\cos }^{2}}x) \)
\( \Leftrightarrow (\cos x+1)[2{{\cos }^{2}}x-1-m\cos x-m(1-\cos x)]=0 \)
\( \Leftrightarrow (\cos x+1)(2{{\cos }^{2}}x-1-m)=0 \).
a) Khi \( m=-2 \) thì (*) thành:
\( (\cos x+1)(2{{\cos }^{2}}x+1)=0\Leftrightarrow \cos x=-1\Leftrightarrow x=\pi +k2\pi ,\text{ }k\in \mathbb{Z} \).
b) Khi \( x\in \left[ 0;\frac{2\pi }{3} \right] \) thì \( \cos x=t\in \left[ -\frac{1}{2};1 \right] \).
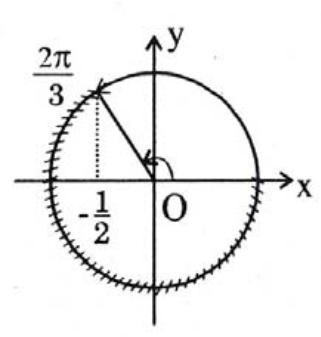
Nhận xét răng với mỗi t trên \( \left[ -\frac{1}{2};1 \right] \) ta chỉ tìm được duy nhất một x trên \( \left[ 0;\frac{2\pi }{3} \right] \).
Yêu cầu bài toán \( \Leftrightarrow 2{{t}^{2}}-1-m=0 \) có đúng hai nghiệm trên \( \left[ -\frac{1}{2};1 \right] \).
Xét \( y=2{{t}^{2}}-1\text{ }(P) \) và \( y=m\text{ }(d) \).
Ta có: \( {y}’=4t\Rightarrow {y}’=0\Leftrightarrow t=0 \).
Bảng biến thiên:
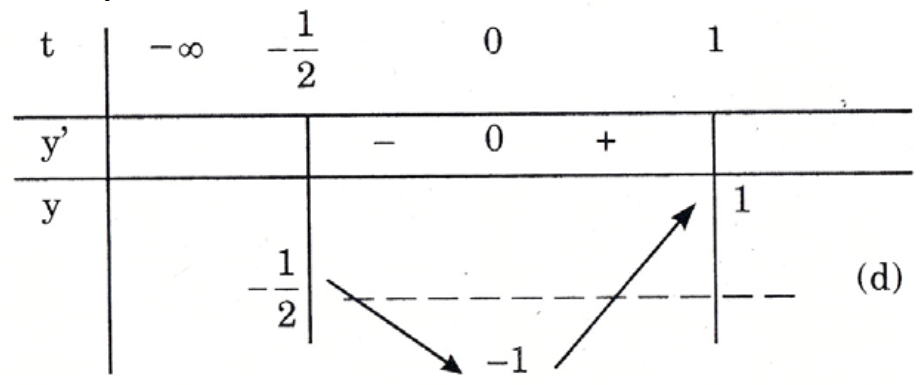
Vậy (*) có đúng hai nghiệm trên \( \left[ 0;\frac{2\pi }{3} \right] \) \( \Leftrightarrow (d) \) cắt (P) tại hai điểm phân biệt trên \( \left[ -\frac{1}{2};1 \right] \)
\( \Leftrightarrow -1<m\le \frac{1}{2} \).
Câu 27. Cho phương trình: \( (1-a){{\tan }^{2}}x-\frac{2}{\cos x}+1+3a=0 \) (*)
a) Giải (*) khi \( a=\frac{1}{2} \).
b) Tìm a để (1) có nhiều hơn một nghiệm trên \( \left( 0;\frac{\pi }{2} \right) \).
Hướng dẫn giải:
Điều kiện: \( \cos x\ne 0\Leftrightarrow x\ne \frac{\pi }{2}+k\pi \) .
(*) \( \Leftrightarrow (1-a){{\sin }^{2}}x-2\cos x+(1+3a){{\cos }^{2}}x=0 \)
\( \Leftrightarrow (1-a)(1-{{\cos }^{2}}x)-2\cos x+(1+3a){{\cos }^{2}}x=0 \)
\( \Leftrightarrow 4a{{\cos }^{2}}x-2\cos x+1-a=0\Leftrightarrow a(4{{\cos }^{2}}x-1)-(2\cos x-1)=0 \)
\( \Leftrightarrow (2\cos x-1)[a(2\cos x+1)-1]=0 \).
a) Khi \( a=\frac{1}{2} \) thì (*) thành: \( \Leftrightarrow (2\cos x-1)\left( \cos x-\frac{1}{2} \right)=0 \)
\( \Leftrightarrow \cos x=\frac{1}{2}=\cos \frac{\pi }{3} \) (nhận do \( \cos x\ne 0 \))
\( \Leftrightarrow x=\pm \frac{\pi }{3}+k2\pi ,\text{ }k\in \mathbb{Z} \).
b) Khi \( x\in \left( 0;\frac{\pi }{2} \right) \) thì \( \cos x=t\in (0;1) \).
Ta có: \( (1)\Leftrightarrow \left[ \begin{align} & \cos x=t=\frac{1}{2}\in (0;1) \\ & 2a\cos x=1-a\begin{matrix} {} & (**) \\\end{matrix} \\ \end{align} \right. \).
Yêu cầu bài toán \( \Leftrightarrow (**) \) có nghiệm trên \( (0;1)\backslash \left\{ \frac{1}{2} \right\}\Leftrightarrow \left\{ \begin{align} & a\ne 0 \\ & 0<\frac{1-a}{2a}<1 \\ & \frac{1-a}{2a}\ne \frac{1}{2} \\ \end{align} \right. \)
\( \Leftrightarrow \left\{ \begin{align} & a\ne 0 \\ & \frac{1-a}{2a}>0 \\ & \frac{1-3a}{2a}<0 \\ & 2(1-a)\ne 2a \\ \end{align} \right. \) \( \Leftrightarrow \left\{ \begin{align} & 0<a<1 \\ & a<0\vee a>\frac{1}{3} \\ & a\ne \frac{1}{2} \\ \end{align} \right. \) \( \Leftrightarrow \left\{ \begin{align} & \frac{1}{3}<a<1 \\ & a\ne \frac{1}{2} \\ \end{align} \right. \).
Cách khác: Đặt \( u=\frac{1}{\cos x} \), điều kiện \( u\ge 1 \), phương trình thành:
\( (1-a)({{u}^{2}}-1)-2u+1+3a=0\Leftrightarrow (1-a){{u}^{2}}-2u+4a=0 \)
\( \Leftrightarrow (u-2)[(1-a)u-2a]=0 \).
Câu 28. Cho phương trình: \( \cos 4x+6\sin x\cos x=m \) (1)
a) Giải (1) khi \( m=1 \).
b) Tìm m để (1) có hai nghiệm phân biệt trên \( \left[ 0;\frac{\pi }{4} \right] \).
Hướng dẫn giải:
Ta có: \( (1)\Leftrightarrow 1-2{{\sin }^{2}}2x+3\sin 2x=m \)
Đặt \( t=\sin 2x \) (điều kiện: \( \left| t \right|\le 1 \)).
Khi đó, phương trình thành: \( 2{{t}^{2}}-3t+m-1=0 \) (2)
a) Khi \( m=1 \) thì (2) thành: \( 2{{t}^{2}}-3t=0 \)
\( \Leftrightarrow \left[ \begin{align} & t=0\text{ }(n) \\ & t=\frac{3}{2}\text{ }(\ell ) \\ \end{align} \right.\Leftrightarrow \sin 2x=0\Leftrightarrow x=\frac{k\pi }{2} \).
b) Khi \( x\in \left[ 0;\frac{\pi }{4} \right] \) thì \( \sin 2x=t\in [0;1] \).
Nhận thấy rằng mỗi t tìm được trên \( [0;1] \) ta chỉ tìm được duy nhất một \( x\in \left[ 0;\frac{\pi }{4} \right] \).
Ta có: \( (2)\Leftrightarrow -2{{t}^{2}}+3t+1=m \).
Xét \( y=-2{{t}^{2}}+3t+1 \) trên \( [0;1] \).
Ta có: \( {y}’=-4t+3 \).
Bảng biến thiên:
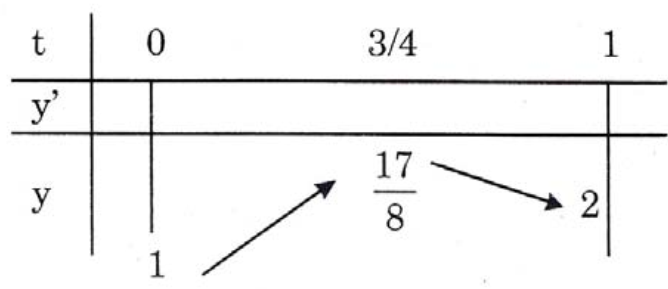
Yêu cầu bài toán \( \Leftrightarrow (d):y=m \)cắt tại hai điểm phân biệt trên \( [0;1] \)
\( \Leftrightarrow 2\le m<\frac{17}{8} \).
Cách khác: Đặt \( f(x)=2{{t}^{2}}-3t+m-1 \). Vì \( a=2>0 \), nên ta có:
Yêu cầu bài toán \( \Leftrightarrow \left\{ \begin{align}& \Delta =17-8m>0 \\ & f(0)=m-1\ge 0 \\ & f(1)=m-2\ge 0 \\ & 0\le \frac{S}{2}=\frac{3}{4}\le 1 \\ \end{align} \right.\Leftrightarrow 2\le m<\frac{17}{8} \).
Câu 29. Cho phương trình: \( 4{{\cos }^{5}}x.sinx-4{{\sin }^{5}}xcosx={{\sin }^{2}}4x+m \) (1)
a) Biết rằng \( x=\pi \) là nghiệm của (1). Hãy giải (1) trong trường hợp đó.
b) Cho biết \( x=-\frac{\pi }{8} \) là một nghiệm của (1). Hãy tìm tất cả nghiệm của (1) thỏa \( {{x}^{4}}-3{{x}^{2}}+2<0 \).
Hướng dẫn giải:
\( (1)\Leftrightarrow 4\sin x\cos x({{\cos }^{4}}x-{{\sin }^{4}}x)={{\sin }^{2}}4x+m \)
\( \Leftrightarrow 2\sin 2x({{\cos }^{2}}x-{{\sin }^{2}}x)({{\cos }^{2}}x+{{\sin }^{2}}x)={{\sin }^{2}}4x+m \)
\( \Leftrightarrow 2\sin 2x.\cos 2x={{\sin }^{2}}4x+m\Leftrightarrow {{\sin }^{2}}4x-\sin 4x+m=0 \) (2)
a) \( x=\pi \) là nghiệm của (1) \( \Rightarrow {{\sin }^{2}}4\pi -\sin 4\pi +m=0\Rightarrow m=0 \).
Lúc đó \( (1)\Leftrightarrow \sin 4x(1-\sin 4x)=0\Leftrightarrow \sin 4x=0\vee \sin 4x=1 \)
\( \Leftrightarrow 4x=k\pi \vee 4x=\frac{\pi }{2}+k2\pi \Leftrightarrow x=\frac{k\pi }{4}\vee x=\frac{\pi }{8}+\frac{k\pi }{2},\text{ }k\in \mathbb{Z} \).
b) \( {{x}^{4}}-3{{x}^{2}}+2<0\Leftrightarrow \left\{ \begin{align} & t={{x}^{2}}\ge 0 \\ & {{t}^{2}}-3t+2<0 \\ \end{align} \right. \)
\( \Leftrightarrow \left\{ \begin{align} & t={{x}^{2}}\ge 0 \\ & 1 < t<2 \\ \end{align} \right. \) \( \Leftrightarrow 1 < \left| x \right| < \sqrt{2}\Leftrightarrow \left[ \begin{align}& -\sqrt{2} < x<-1 \\ & 1 < x <\sqrt{2} \\ \end{align} \right. \) .
\( x=-\frac{\pi }{8} \) thì \( \sin 4x=\sin \left( -\frac{\pi }{2} \right)=-1 \).
\( x=-\frac{\pi }{8} \) là nghiệm của \( (1)\Rightarrow 1+1+m=0\Leftrightarrow m=-2 \).
Lúc đó (2) thành: \( {{\sin }^{2}}4x-\sin 4x-2=0 \)
\( \Leftrightarrow \left[ \begin{align} & \sin 4x=-1\text{ }(n) \\ & \sin 4x=2\text{ }(\ell ) \\ \end{align} \right.\Leftrightarrow \sin 4x=-1 \)
\(\Leftrightarrow 4x=-\frac{\pi }{2}+k2\pi \Leftrightarrow x=-\frac{\pi }{8}+\frac{k\pi }{2}\).
Kết hợp với điều kiện (*) suy ra \( k=1 \).
Vậy (1) có nghiệm \(x=-\frac{\pi }{8}+\frac{\pi }{2}=\frac{3\pi }{8}\) thỏa \( {{x}^{4}}-3{{x}^{2}}+2<0 \).
Câu 30. Tìm a để hai phương trình sau tương đương:
\( 2\cos x.\cos 2x=1+\cos 2x+\cos 3x \) (1)
\( 4{{\cos }^{2}}x-cos3x=a\cos x+(4-a)(1+\cos 2x) \) (2)
Hướng dẫn giải:
Ta có: \( (1)\Leftrightarrow \cos 3x+\cos x=1+\cos 2x+\cos 3x \)
\( \Leftrightarrow \cos x=1+(2{{\cos }^{2}}x-1)\Leftrightarrow \cos x(1-2\cos x)=0 \)
\( \Leftrightarrow \left[ \begin{align} & \cos x=0 \\ & \cos x=\frac{1}{2} \\ \end{align} \right. \).
Ta có: \( (2)\Leftrightarrow 4{{\cos }^{2}}x-(4{{\cos }^{3}}x-3\cos x)=a\cos x+(4-a).2{{\cos }^{2}}x \)
\( \Leftrightarrow 4{{\cos }^{3}}x+(4-2a)co{{s}^{2}}x(a-3)cosx=0 \)
\( \Leftrightarrow \left[ \begin{align} & \cos x=0 \\ & 4{{\cos }^{2}}x+2(2-a)\cos x+a-3=0 \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & \cos x=0 \\ & \left( \cos x-\frac{1}{2} \right)[2\cos x+3-a]=0 \\ \end{align} \right. \)
\( \Leftrightarrow \left[ \begin{align} & \cos x=0 \\ & \cos x=\frac{1}{2} \\ & \cos x=\frac{a-3}{2} \\ \end{align} \right. \).
Vậy yêu cầu bài toán \( \Leftrightarrow \left[ \begin{align} & \frac{a-3}{2}=0 \\ & \frac{a-3}{2}=\frac{1}{2} \\ & \frac{a-3}{2}<-1\vee \frac{a-3}{2}>1 \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & a=3 \\ & a=4 \\ & a<1\vee a>5 \\ \end{align} \right. \).
Câu 31. Cho phương trình: \( \cos 4x={{\cos }^{2}}3x+a{{\sin }^{2}}x \) (*)
a) Giải phương trình khi \( a=1 \).
b) Tìm a để (*) có nghiệm trên \( \left( 0;\frac{\pi }{12} \right) \).
Hướng dẫn giải:
Ta có: (*) \( \Leftrightarrow \cos 4x=\frac{1}{2}(1+\cos 6x)+\frac{a}{2}(1-\cos 2x) \)
\( \Leftrightarrow 2(2{{\cos }^{2}}2x-1)=1+4{{\cos }^{3}}2x-3\cos 2x+a(1-\cos 2x) \) (**)
Đặt \( t=\cos 2x \) (điều kiện: \( \left| t \right|\le 1 \)).
Phương trình (**) trở thành: \( -4{{t}^{3}}+4{{t}^{2}}+3t-3=a(1-t) \)
\( \Leftrightarrow (t-1)(-4{{t}^{2}}+3)=a(1-t) \) (***)
a) Khi \( a=1 \) thì (***) thành: \( (t-1)(-4{{t}^{2}}+4)=0\Leftrightarrow t=\pm 1 \)
\( \Leftrightarrow \cos 2x=\pm 1\Leftrightarrow {{\cos }^{2}}2x=1\Leftrightarrow \sin 2x=0\Leftrightarrow 2x=k\pi \Leftrightarrow x=\frac{k\pi }{2},\text{ }k\in \mathbb{Z} \).
b) Ta có: \( x\in \left( 0;\frac{\pi }{12} \right)\Leftrightarrow 2x\in \left( 0;\frac{\pi }{6} \right) \).
Vậy \( \cos 2x=t\in \left( \frac{\sqrt{3}}{2};1 \right) \).
Vậy (***) \( \Leftrightarrow (t-1)(-4{{t}^{2}}+3)=a(1-t)\Leftrightarrow 4{{t}^{2}}-3=a\text{ }(do\text{ }t\ne 1) \)
Xét \( y=4{{t}^{2}}-3\text{ }(P) \) trên \( \left( \frac{\sqrt{3}}{2};1 \right) \)
\( \Rightarrow {y}’=8t>0,\forall t\in \left( \frac{\sqrt{3}}{2};1 \right) \).
Do đó (*) có nghiệm trên \( \left( 0;\frac{\pi }{2} \right)\Leftrightarrow (d):y=a \) cắt (P) trên \( \left( \frac{\sqrt{3}}{2};1 \right) \)
\( \Leftrightarrow y\left( \frac{\sqrt{3}}{2} \right)<a<y(1)\Leftrightarrow 0<a<1 \).
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









