A. Phương pháp giải
\( a(\sin x+\cos x)+b\sin x\cos x=c \) (1)
Cách giải:
Đặt \( t=\sin x+\cos x \) với điều kiện \( \left| t \right|\le \sqrt{2} \).
Thì \( t=\sqrt{2}\sin \left( x+\frac{\pi }{4} \right)=\sqrt{2}\cos \left( x-\frac{\pi }{4} \right) \).
Ta có: \( {{t}^{2}}=1+2\sin x\cos x \) nên (1) thành: \( at+\frac{b}{2}({{t}^{2}}-1)=c\Leftrightarrow b{{t}^{2}}+2at-b-2c=0 \).
Giải (2) tìm được t, rồi so với điều kiện \( \left| t \right|\le \sqrt{2} \).
Giải phương trình: \( \sqrt{2}\sin \left( x+\frac{\pi }{4} \right)=t \), ta tìm được x.
Chú ý:
+ Phương trình giả đối xứng: \( a(\sin x-\cos x)+b\sin x\cos x=0 \).
Đặt \( t=\sin x-\cos x \) \( \Rightarrow t=\sqrt{2}\sin \left( x-\frac{\pi }{4} \right)=-\sqrt{2}\cos \left( x+\frac{\pi }{4} \right) \)(với điều kiện \( \left| t \right|\le \sqrt{2} \))
Thì \( {{t}^{2}}=1-2\sin x\cos x \).
+ Phương trình lượng giác dạng
\( a(\tan x\pm \cot x)+b({{\tan }^{2}}x+{{\cot }^{2}}x)=0 \)
Ta đặt \( t=\tan x\pm \cot x \) thì \( {{t}^{2}}={{\tan }^{2}}x+{{\cot }^{2}}x\pm 2 \)
Khi \( t=\tan x+\cot x=\frac{2}{\sin 2x} \) thì \( \left| t \right|\ge 2 \) (do \( \left| \sin 2x \right|\le 1 \))
B. Bài tập có lời giải chi tiết
Câu 1. Giải phương trình: \( \sin x+{{\sin }^{2}}x+{{\cos }^{3}}x=0 \) (*)
Lời giải:
(*) \( \Leftrightarrow \sin x(1+\sin x)+\cos x(1-{{\sin }^{2}}x)=0 \)
\( \Leftrightarrow \sin x(1+\sin x)+\cos x(1-\sin x)(1+\sin x)=0 \)
\( \Leftrightarrow (1+\sin x)\left[ \sin x+\cos x(1-\sin x) \right]=0\Leftrightarrow \left[ \begin{align} & \sin x=-1\begin{matrix} {} & {} & (1) \\\end{matrix} \\ & \sin x+\cos x-\sin x\cos x=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right. \).
+ \( (1)\Leftrightarrow x=-\frac{\pi }{2}+k2\pi ,\text{ }k\in \mathbb{Z} \).
+ Xét (2): Đặt \( t=\sin x+\cos x=\sqrt{2}\cos \left( x-\frac{\pi }{4} \right) \), điều kiện \( \left| t \right|\le \sqrt{2} thì {{t}^{2}}=1+2\sin x\cos x \).
Vậy (2) thành: \( t-\frac{{{t}^{2}}-1}{2}=0\Leftrightarrow {{t}^{2}}-2t-1=0 \)
\( \Leftrightarrow \left[ \begin{align} & t=1-\sqrt{2}\text{ }(n) \\ & t=1+\sqrt{2}\text{ }(\ell ) \\ \end{align} \right.\Rightarrow \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=1-\sqrt{2} \)
\( \Leftrightarrow \cos \left( x-\frac{\pi }{4} \right)=\frac{\sqrt{2}}{2}-1 \) \( \Leftrightarrow x-\frac{\pi }{4}=\pm \arccos \left( \frac{\sqrt{2}}{2}-1 \right)+h2\pi \)
\( \Leftrightarrow x=\frac{\pi }{4}\pm \arccos \left( \frac{\sqrt{2}}{2}-1 \right)+h2\pi ,\text{ }h\in \mathbb{Z} \).
Câu 2. Giải phương trình: \( -1+{{\sin }^{3}}x+{{\cos }^{3}}x=\frac{3}{2}\sin 2x \) (*)
Lời giải:
(*) \( \Leftrightarrow -1+(\sin x+\cos x)(1-\sin x\cos x)=\frac{3}{2}.2\sin x\cos x \).
Đặt \( t=\sin x+\cos x=\sqrt{2}\sin \left( x+\frac{\pi }{4} \right) \), với điều kiện \( \left| t \right|\le \sqrt{2} thì {{t}^{2}}=1+2\sin x\cos x \).
Vậy (*) thành: \( -1+t\left( 1-\frac{{{t}^{2}}-1}{2} \right)=\frac{3}{2}({{t}^{2}}-1) \)
\( \Leftrightarrow -2+t(3-{{t}^{2}})=3({{t}^{2}}-1)\Leftrightarrow {{t}^{3}}+3{{t}^{2}}-3t-1=0 \)
\( \Leftrightarrow (t-1)({{t}^{2}}+4t+1)=0\Leftrightarrow \left[ \begin{align} & t=1\text{ }(n) \\ & t=-2+\sqrt{3}\text{ }(n) \\ & t=-2-\sqrt{3}\text{ }(\ell ) \\ \end{align} \right. \).
+ Với \( t=1\Rightarrow \sin \left( x+\frac{\pi }{4} \right)=\frac{1}{\sqrt{2}}=\sin \frac{\pi }{4} \)
\(\Leftrightarrow \left[ \begin{align} & x+\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \\ & x+\frac{\pi }{4}=\frac{3\pi }{4}+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=k2\pi \\ & x=\frac{\pi }{2}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \)
+ Với \( t=\sqrt{3}-2\Rightarrow \sin \left( x+\frac{\pi }{4} \right)=\frac{\sqrt{3}-2}{\sqrt{2}} \)
\( \Leftrightarrow \left[ \begin{align} & x+\frac{\pi }{4}=\arcsin \left( \frac{\sqrt{3}-2}{\sqrt{2}} \right)+h2\pi \\ & x+\frac{\pi }{4}=\pi -\arcsin \left( \frac{\sqrt{3}-2}{\sqrt{2}} \right)+h2\pi \\ \end{align} \right. \)
\( \Leftrightarrow \left[ \begin{align} & x=-\frac{\pi }{4}+\arcsin \left( \frac{\sqrt{3}-2}{\sqrt{2}} \right)+h2\pi \\ & x=\frac{3\pi }{4}-\arcsin \left( \frac{\sqrt{3}-2}{\sqrt{2}} \right)+h2\pi \\ \end{align} \right.,\text{ }h\in \mathbb{Z} \).
Câu 3. Giải phương trình \( \sqrt{2}(\sin x+\cos x)=\tan x+\cot x \) (*)
Lời giải:
Điều kiện: \( \left\{ \begin{align} & \sin x\ne 0 \\ & \cos x\ne 0 \\ \end{align} \right.\Leftrightarrow \sin 2x\ne 0 \).
Lúc đó: (*)\(\Leftrightarrow \sqrt{2}(\sin x+\cos x)=\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}\)
\( \sqrt{2}(\sin x+\cos x)=\frac{{{\sin }^{2}}x+{{\cos }^{2}}x}{\sin x\cos x}=\frac{1}{\sin x\cos x} \).
Đặt \( t=\sin x+\cos x=\sqrt{2}\sin \left( x+\frac{\pi }{4} \right) \) thì:
\( {{t}^{2}}=1+2\sin x\cos x\Rightarrow \sin x\cos x=\frac{{{t}^{2}}-1}{2} \) với \( \left| t \right|\le \sqrt{2} \)và \( {{t}^{2}}\ne 1 \) .
(*) thành \( \sqrt{2}t=\frac{2}{{{t}^{2}}-1}\Leftrightarrow \sqrt{2}{{t}^{3}}-\sqrt{2}t-2=0 \) (Hiển nhiên \( t=\pm 1 \) không là nghiệm)
\( \Leftrightarrow (t-\sqrt{2})(\sqrt{2}{{t}^{2}}+2t+\sqrt{2})=0\Leftrightarrow \left[ \begin{align} & t=\sqrt{2} \\ & {{t}^{2}}+\sqrt{2}t+1=0\text{ }(\text{vô nghiệm }) \\ \end{align} \right. \).
Vậy (*) \( \Leftrightarrow \sqrt{2}\sin \left( x+\frac{\pi }{4} \right)=\sqrt{2}\Leftrightarrow \sin \left( x+\frac{\pi }{4} \right)=1\Leftrightarrow x+\frac{\pi }{4}=\frac{\pi }{2}+k2\pi \)
\( \Leftrightarrow x=\frac{\pi }{4}+k2\pi ,\text{ }k\in \mathbb{Z} \).
Câu 4. Giải phương trình: \( 3(\cot x-\cos x)-5(\tan x-\sin x)=2 \) (*)
Lời giải:
Với điều kiện \( \sin 2x\ne 0 \), nhân 2 vế phương trình cho \( \sin x\cos x\ne 0 \) thì:
(*) \( \Leftrightarrow 3{{\cos }^{2}}x(1-sinx)-5{{\sin }^{2}}x(1-cosx)=2sinxcosx \)
\( \Leftrightarrow 3\cos x\left[ \cos x(1-\sin x)+\sin x \right]-5\sin x\left[ \sin x(1-\cos x)+\cos x \right]=0 \)
\( \Leftrightarrow 3\cos x(\cos x-\sin x\cos x+\sin x)-5\sin x(\sin x-\sin x\cos x+\cos x)=0 \)
\( \Leftrightarrow \left[ \begin{align} & \sin x+\cos x-\sin x\cos x=0\begin{matrix} {} & (1) \\\end{matrix} \\ & 3\cos x-5\sin x=0\begin{matrix} {} & {} & {} & (2) \\\end{matrix} \\ \end{align} \right. \).
(Ghi chú: \( A.B+A.C=A.D\Leftrightarrow \left[ \begin{align} & A=0 \\ & B+C=D \\ \end{align} \right. \))
+ Giải (1): Đặt \( t=\sin x+\cos x=\sqrt{2}\sin \left( x+\frac{\pi }{4} \right) \) thì
\( {{t}^{2}}=1+2\sin x\cos x \) với điều kiện: \( \left| t \right|\le \sqrt{2} \) và \( t\ne \pm 1 \).
(1) thành: \( t-\frac{{{t}^{2}}-1}{2}=0\Leftrightarrow {{t}^{2}}-2t-1=0 \)
\( \Leftrightarrow \left[ \begin{align} & t=1+\sqrt{2}\text{ }(\ell ) \\ & t=1-\sqrt{2}\text{ }(n) \\ \end{align} \right. \)
Vậy: \( \sqrt{2}\sin \left( x+\frac{\pi }{4} \right)=1-\sqrt{2}\Leftrightarrow \sin \left( x+\frac{\pi }{4} \right)=\frac{1-\sqrt{2}}{2} \)
\( \Leftrightarrow \left[ \begin{align} & x+\frac{\pi }{4}=\arcsin \left( \frac{1-\sqrt{2}}{2} \right)+k2\pi \\ & x+\frac{\pi }{4}=\pi -\arcsin \left( \frac{1-\sqrt{2}}{2} \right)+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=-\frac{\pi }{4}+\arcsin \left( \frac{1-\sqrt{2}}{2} \right)+k2\pi \\ & x=\frac{3\pi }{4}-\arcsin \left( \frac{1-\sqrt{2}}{2} \right)+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
+ Giải (2) \( \Leftrightarrow \tan x=\frac{3}{5}\Leftrightarrow x=\arctan \left( \frac{3}{5} \right)+h\pi ,\text{ }h\in \mathbb{Z} \).
Câu 5. Giải phương trình: \( 3{{\tan }^{3}}-\tan x+\frac{3(1+\sin x)}{{{\cos }^{2}}x}=8{{\cos }^{2}}\left( \frac{\pi }{4}-\frac{x}{2} \right) \) (*)
Lời giải:
Điều kiện: \( \cos x\ne 0\Leftrightarrow \sin x\ne \pm 1 \).
Lúc đó: (*) \( \Leftrightarrow \tan x(3{{\tan }^{2}}x-1)+3(1+\sin x)(1+{{\tan }^{2}}x)=4\left[ 1+\cos \left( \frac{\pi }{2}-x \right) \right]=4(1+\sin x) \)
\(\Leftrightarrow \tan x(3{{\tan }^{2}}x-1)+(1+\sin x)\left[ 3(1+{{\tan }^{2}}x)-4 \right]=0\)
\(\Leftrightarrow (3{{\tan }^{2}}x-1)(\tan x+1+\sin x)=0\Leftrightarrow (3{{\tan }^{2}}x-1)(\sin x+\cos x+\sin x\cos x)=0\)
\( \Rightarrow \left[ \begin{align} & 3{{\tan }^{2}}x=1\begin{matrix} {} & {} & {} & (1) \\\end{matrix} \\ & \sin x+\cos x+\sin x\cos x=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right. \)
+ Giải (1) \( \Leftrightarrow {{\tan }^{2}}x=\frac{1}{3}\Leftrightarrow \tan x=\pm \frac{\sqrt{3}}{3}\Leftrightarrow x=\pm \frac{\pi }{6}+k\pi ,\text{ }k\in \mathbb{Z} \).
+ Giải (2): Đặt \( t=\sin x+\cos x=\sqrt{2}\sin \left( x+\frac{\pi }{4} \right) \), với điều kiện \( \left| t \right|\le \sqrt{2} \) và \( t\ne \pm 1 \).
Thì \( {{t}^{2}}=1+2\sin x\cos x \)
(2) thành: \( t+\frac{{{t}^{2}}-1}{2}=0\Leftrightarrow {{t}^{2}}+2t-1=0\Leftrightarrow \left[ \begin{align} & t=-1-\sqrt{2}\text{ }(\ell ) \\ & t=-1+\sqrt{2}\text{ }(n) \\ \end{align} \right. \)
\( \Rightarrow \sqrt{2}\sin \left( x+\frac{\pi }{4} \right)=\sqrt{2}-1\Leftrightarrow \sin \left( x+\frac{\pi }{4} \right)=\frac{\sqrt{2}-1}{\sqrt{2}} \)
\( \Leftrightarrow \left[ \begin{align} & x+\frac{\pi }{4}=\arcsin \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ & x+\frac{\pi }{4}=\pi -\arcsin \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=-\frac{\pi }{4}+\arcsin \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ & x=-\frac{3\pi }{4}-\arcsin \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
Câu 6. Giải phương trình: \( 2{{\sin }^{3}}x-\sin x=2{{\cos }^{3}}x-\cos x+\cos 2x \) (*)
Lời giải:
(*) \( \Leftrightarrow 2({{\sin }^{3}}x-{{\cos }^{3}}x)-(\sin x-\cos x)+{{\sin }^{2}}x-{{\cos }^{2}}x=0 \)
\( \Leftrightarrow 2(\sin x-\cos x)({{\sin }^{2}}x+sinxcosx+co{{s}^{2}}x)-(\sin x-\cos x)+(\sin x-\cos x)(\sin x+\cos x)=0 \)
\(\Leftrightarrow \left[ \begin{align} & \sin x-\cos x=0\begin{matrix} {} & {} & {} & (1) \\\end{matrix} \\ & 2(1+\sin x\cos x)-1+(\sin x+\cos x)=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right.\)
+ \( (1)\Leftrightarrow \tan x=1\Leftrightarrow x=\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
+ Xét (2) đặt: \( t=\sin x+\cos x=\sqrt{2}\cos \left( x-\frac{\pi }{4} \right)\), với điều kiện: \( \left| t \right|\le \sqrt{2} \) .
Khi đó: \( {{t}^{2}}=1+\sin 2x \).
Vậy (2) thành: \( t+({{t}^{2}}-1)+1=0\Leftrightarrow t(t+1)=0\Leftrightarrow t=0\vee t=-1 \)
Với \( t=0\Rightarrow \cos \left( x-\frac{\pi }{4} \right)=0\Leftrightarrow x-\frac{\pi }{4}=\frac{\pi }{2}+k\pi \Leftrightarrow x=\frac{3\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Với \( t=-1\Rightarrow \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=-1\Leftrightarrow \cos \left( x-\frac{\pi }{4} \right)=-\frac{\sqrt{2}}{2}=\cos \frac{3\pi }{4} \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\frac{3\pi }{4}+k2\pi \\ & x-\frac{\pi }{4}=-\frac{3\pi }{4}+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=\pi +k2\pi \\ & x=-\frac{\pi }{2}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
Câu 7. Giải phương trình: \( \sin x+{{\sin }^{2}}x+si{{n}^{3}}x+si{{n}^{4}}x=cosx+co{{s}^{2}}x+co{{s}^{3}}x+co{{s}^{4}}x \) (*)
Lời giải:
Ta có: (*) \( \Leftrightarrow (\sin x-\cos x)+({{\sin }^{2}}x-co{{s}^{2}}x)+({{\sin }^{3}}x-co{{s}^{3}}x)+({{\sin }^{4}}x-co{{s}^{4}}x)=0 \)
\( \Leftrightarrow (\sin x-\cos x)+(\sin x-cosx)(\sin x+\cos x)+(\sin x-cosx)(1+\sin x\cos x) \)
\( +(\sin x-cosx)(\sin x+\cos x)=0 \).
\( \Leftrightarrow \left[ \begin{align} & \sin x-\cos x=0 \\ & 1+(\sin x+\cos x)+(1+\sin x.\cos x)+(\sin x+\cos x)=0 \\ \end{align} \right. \)
\( \Leftrightarrow \left[ \begin{align} & \sin x-\cos x=0\begin{matrix} {} & {} & {} & (1) \\\end{matrix} \\ & 2(\sin x+\cos x)+\sin x\cos x+2=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right. \).
+ Giải (1) \( \Leftrightarrow \tan x=1\Leftrightarrow x=\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
+ Giải (2): Đặt \( t=\sin x+\cos x=\sqrt{2}\cos \left( x-\frac{\pi }{4} \right) \), với điều kiện \( \left| t \right|\le \sqrt{2} \) thì
\( {{t}^{2}}=1+2sinxcosx \)
(2) thành: \( 2t+\frac{{{t}^{2}}-1}{2}+2=0\Leftrightarrow {{t}^{2}}+4t+3=0\Leftrightarrow \left[ \begin{align} & t=-1\text{ }(n) \\ & t=-3\text{ }(\ell ) \\ \end{align} \right. \).
\( \Rightarrow \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=-1\Leftrightarrow \cos \left( x-\frac{\pi }{4} \right)=-\frac{\sqrt{2}}{2}=\cos \frac{3\pi }{4} \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\frac{3\pi }{4}+k2\pi \\ & x-\frac{\pi }{4}=-\frac{3\pi }{4}+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=\pi +k2\pi \\ & x=-\frac{\pi }{2}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
Câu 8. Giải phương trình: \( {{\tan }^{2}}x(1-{{\sin }^{3}}x)+{{\cos }^{3}}x-1=0 \) (*)
Lời giải:
Điều kiện: \( \cos x\ne 0\Leftrightarrow \sin x\ne \pm 1 \).
Lúc đó (*) \( \Leftrightarrow \frac{{{\sin }^{2}}x}{{{\cos }^{2}}x}(1-{{\sin }^{3}}x)+{{\cos }^{3}}x-1=0 \)
\( \Leftrightarrow (1-{{\cos }^{2}}x)(1-{{\sin }^{3}}x)-(1-{{\cos }^{3}}x)(1-{{\sin }^{2}}x)=0 \)
\( \Leftrightarrow (1-\cos x)(1+\cos x)(1-{{\sin }^{3}}x)(1+\sin x+{{\sin }^{2}}x) \)
\( -(1-\cos x)(1+\cos x+{{\cos }^{2}}x)(1-\sin x)(1+\sin x)=0 \)
\( \Leftrightarrow (1-\cos x)(1-\sin x)\left[ (1+\cos x)(1+\sin x+{{\sin }^{2}}x)-(1+\cos x+{{\cos }^{2}}x)(1+\sin x) \right]=0 \)
\(\Leftrightarrow \left[ \begin{align} & 1-\cos x=0 \\ & 1-\sin x=0 \\ & (1+\cos x)(1+\sin x+{{\sin }^{2}}x)-(1+\cos x+{{\cos }^{2}}x)(1+\sin x)=0 \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & \cos x=1\text{ }(n) \\ & \sin x=1\text{ }(\ell ) \\ & 1+\sin x+{{\sin }^{2}}x+\cos x+\cos x.\sin x+\cos x.{{\sin }^{2}}x \\ & -(1+\cos x+{{\cos }^{2}}x+\sin x+\cos x\sin x+{{\cos }^{2}}x\sin x)=0 \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & \cos x=1\begin{matrix} {} & {} & {} & {} \\\end{matrix}(1) \\ & {{\sin }^{2}}x+{{\sin }^{2}}x\cos x-{{\cos }^{2}}x-\sin x{{\cos }^{2}}x=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right.\).
+ Giải \( (1)\Leftrightarrow x=k2\pi ,\text{ }k\in \mathbb{Z} \).
+ Giải \( \Leftrightarrow {{\sin }^{2}}x-co{{s}^{2}}x+\sin x\cos x(\sin x-\cos x)=0 \)
\( \Leftrightarrow (\sin x-\cos x)(\sin x+\cos x)+\sin x\cos x(\sin x-\cos x)=0 \)
\( \Leftrightarrow (\sin x-\cos x)(\sin x+\cos x+\sin x\cos x)=0\Leftrightarrow \left[ \begin{align} & \sin x-\cos x=0\begin{matrix} {} & {} & {} & {} \\\end{matrix}(3) \\ & \sin x+\cos x+\sin x\cos x=0\begin{matrix} {} & (4) \\\end{matrix} \\ \end{align} \right. \).
Với phương trình \( (3)\Leftrightarrow \sin x=\cos x\Leftrightarrow \tan x=1\Leftrightarrow x=\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Với phương trình (4), ta đặt \( t=\sin x+\cos x=\sqrt{2}\cos x\left( x-\frac{\pi }{4} \right) \) (điều kiện \( \left| t \right|\le \sqrt{2} \) và \( t\ne \pm 1 \)).
\( \Rightarrow {{t}^{2}}=1+2\sin x\cos x \).
Ta được phương trình: \( t+\frac{{{t}^{2}}-1}{2}=0\Leftrightarrow {{t}^{2}}+2t-1=0\Leftrightarrow \left[ \begin{align} & t=-1-\sqrt{2}\text{ }(\ell ) \\ & t=-1+\sqrt{2}\text{ }(n) \\ \end{align} \right. \)
Vậy \( \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=\sqrt{2}-1\Leftrightarrow \cos \left( x-\frac{\pi }{4} \right)=\frac{\sqrt{2}-1}{\sqrt{2}} \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\arccos \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ & x-\frac{\pi }{4}=-\arccos \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{4}+\arccos \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ & x=\frac{\pi }{4}-\arccos \left( \frac{\sqrt{2}-1}{\sqrt{2}} \right)+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
Câu 9. Cho phương trình \( m(\sin x+\cos x+1)=1+\sin 2x \) (*). Tìm m để phương trình có nghiệm thuộc đoạn \( \left[ 0;\frac{\pi }{2} \right] \).
Lời giải:
Đặt \( t=\sin x+\cos x=\sqrt{2}\sin \left( x+\frac{\pi }{4} \right) \), điều kiện: \( \left| t \right|\le \sqrt{2} \)
Thì \( {{t}^{2}}=1+\sin 2x \).
Vậy (*) thành: \( m(t+1)={{t}^{2}} \).
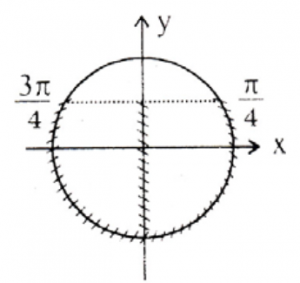
Nếu \( 0\le x\le \frac{\pi }{2} \) thì \( \frac{\pi }{4}\le x+\frac{\pi }{4}\le \frac{3\pi }{4} \).
Do đó: \( \frac{\sqrt{2}}{2}\le \sin \left( x+\frac{\pi }{4} \right)\le 1\Leftrightarrow 1\le t\le \sqrt{2} \).
Ta có: \( m(t+1)={{t}^{2}}\Leftrightarrow m=\frac{{{t}^{2}}}{t+1} \) (do \( t=-1 \) không là nghiệm của phương trình).
Xét \( y=\frac{{{t}^{2}}}{t+1} \) trên \( \left[ 1;\sqrt{2} \right] \) thì \( {y}’=\frac{{{t}^{2}}+2t}{{{(t+1)}^{2}}}>0,\text{ }\forall t\in \left[ 1;\sqrt{2} \right] \).
Do đó, y đồng biến trên \( \left[ 1;\sqrt{2} \right] \).
Vậy (*) có nghiệm trên \( \left[ 1;\frac{\pi }{2} \right] \) \( \Leftrightarrow y(1)\le m\le y(\sqrt{2})\Leftrightarrow \frac{1}{2}\le m\le 2\left( \sqrt{2}-1 \right) \).
Câu 10. Cho phương trình \( {{\cos }^{3}}x+{{\sin }^{3}}x=m\sin x\cos x \) (*)
a) Giải phương trình khi \( m=\sqrt{2} \).
b) Tìm m để (*) có nghiệm.
Lời giải:
Ta có: (*) \( \Leftrightarrow (\cos x+\sin x)(1-\sin x\cos x)=m\sin x\cos x \).
Đặt \( t=\sin x+\cos x=\sqrt{2}\cos \left( x-\frac{\pi }{4} \right) \), với điều kiện \( \left| t \right|\le \sqrt{2} \)
Thì \( {{t}^{2}}=1+2\sin x\cos x \)
Vậy (*) thành \( t\left( 1-\frac{{{t}^{2}}-1}{2} \right)=m.\frac{{{t}^{2}}-1}{2}\Leftrightarrow t(3-{{t}^{2}})=m({{t}^{2}}-1) \).
a) Khi \( m=\sqrt{2} \) ta có phương trình: \( t(3-{{t}^{2}})=\sqrt{2}({{t}^{2}}-1) \)
\( \Leftrightarrow {{t}^{3}}+\sqrt{2}{{t}^{2}}-3t-\sqrt{2}=0\Leftrightarrow \left( t-\sqrt{2} \right)\left( {{t}^{2}}+2\sqrt{2}t+1 \right)=0 \)
\( \Leftrightarrow \left[ \begin{align} & t=\sqrt{2}\text{ }(n) \\ & t=-\sqrt{2}+1\text{ }(n) \\ & t=-\sqrt{2}-1\text{ }(\ell ) \\ \end{align} \right. \)
+ Với \( t=\sqrt{2}\Rightarrow \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=1\Leftrightarrow \cos \left( x-\frac{\pi }{4} \right)=\frac{\sqrt{2}}{2}=\cos \frac{\pi }{4} \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \\ & x-\frac{\pi }{4}=-\frac{\pi }{4}+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{2}+k2\pi \\ & x=k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
+ Với \( t=1-\sqrt{2}\Rightarrow \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=1-\sqrt{2}\Leftrightarrow \cos \left( x-\frac{\pi }{4} \right)=\frac{1-\sqrt{2}}{\sqrt{2}} \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\arccos \left( \frac{1-\sqrt{2}}{\sqrt{2}} \right)+k2\pi \\ & x-\frac{\pi }{4}=-\arccos \left( \frac{1-\sqrt{2}}{\sqrt{2}} \right)+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{4}+\arccos \left( \frac{1-\sqrt{2}}{\sqrt{2}} \right)+k2\pi \\ & x=\frac{\pi }{4}-\arccos \left( \frac{1-\sqrt{2}}{\sqrt{2}} \right)+k2\pi \\ \end{align} \right.,k\in \mathbb{Z} \).
b) Xét phương trình: \( t(3-{{t}^{2}})=m({{t}^{2}}-1) \) (**)
Do \( t=\pm 1 \) không là nghiệm của (**) nên
(**) \( \Leftrightarrow m=\frac{3t-{{t}^{3}}}{{{t}^{2}}-1} \).
Xét \( y=\frac{3t-{{t}^{3}}}{{{t}^{2}}-1} \) (C) trên \( \left[ -\sqrt{2};\sqrt{2} \right]\backslash \{\pm 1\} \).
Ta có: \( {y}’=\frac{-{{t}^{4}}-3}{{{({{t}^{2}}-1)}^{2}}}<0,\text{ }\forall t\ne \{\pm 1\} \).
Suy ra y giảm trên \( (-1;1) \) và \( \underset{x\to -{{1}^{+}}}{\mathop{\lim }}\,y=+\infty ,\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,y=-\infty \) .
Do đó trên \( (-1;1)\subset \left[ -\sqrt{2};\sqrt{2} \right]\backslash \{\pm 1\} \), ta có: \( (d):y=m \) cắt \( (C):y=\frac{3t-{{t}^{3}}}{{{t}^{2}}-1},\text{ }\forall m\in \mathbb{R} \).
Vậy (*) có nghiệm \( \forall m\in \mathbb{R} \).
Câu 11. Cho phương trình: \( m(\sin x+\cos x)+1+\frac{1}{2}\left( \tan x+\cot x+\frac{1}{\sin x}+\frac{1}{\cos x} \right)=0 \) (*)
a) Giải phương trình khi \( m=\frac{1}{2} \).
b) Tìm m để (*) có nghiệm trên \( \left( 0;\frac{\pi }{2} \right) \).
Lời giải:
Với điều kiện: \( \sin 2x\ne 0 \).
Ta có: (*) \( \Leftrightarrow m(\sin x+\cos x)+1+\frac{1}{2}\left( \frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}+\frac{1}{\sin x}+\frac{1}{\cos x} \right)=0 \)
\(\Leftrightarrow m(\sin x+\cos x)+1+\frac{{{\sin }^{2}}x+{{\cos }^{2}}x+\sin x+\cos x}{2\sin x\cos x}=0\)
\( \Leftrightarrow m\sin 2x(\sin x+\cos x)+\sin 2x+(1+\cos x+\sin x)=0 \)
\( \Leftrightarrow m\sin 2x(\sin x+\cos x)+{{(\sin x+\cos x)}^{2}}+\sin x+\cos x=0 \)
\( \Leftrightarrow (\sin x+\cos x)\left[ m\sin 2x+\sin x+\cos x+1 \right]=0 \)
\( \Leftrightarrow \left[ \begin{align} & \sin x+\cos x=0\begin{matrix} {} & {} & {} & (1) \\\end{matrix} \\ & m\sin 2x+\sin x+\cos x+1=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right. \).
Xét (2) đặt \( t=\sin x+\cos x=\sqrt{2}\cos \left( x-\frac{\pi }{4} \right) \) thì \( {{t}^{2}}=1+\sin 2x \).
Do \( \sin 2x\ne 0 \) nên \( \left| t \right|\le \sqrt{2} \) và \( t\ne \pm 1 \).
Vậy (*) thành: \( \left[ \begin{align} & t=0 \\ & m({{t}^{2}}-1)+t+1=0 \\ \end{align} \right. \)
\( \Leftrightarrow \left[ \begin{align} & t=0\text{ }(n) \\ & m(t-1)+1=0\text{ }(do\text{ }t\ne -1) \\ \end{align} \right. \).
a) Khi \( m=\frac{1}{2} \) thì ta được:
\(\left[ \begin{align} & t=0 \\ & t=-1\text{ }(\ell ) \\ \end{align} \right.\Rightarrow \sin x+\cos x=0\Leftrightarrow \tan x=-1\)
\( \Leftrightarrow x=-\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
b) Ta có: \( 0<x<\frac{\pi }{2}\Leftrightarrow -\frac{\pi }{4}<x-\frac{\pi }{4}<\frac{\pi }{4} \).
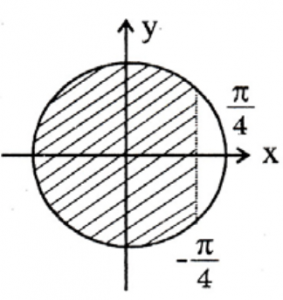
Lúc đó: \( \frac{\sqrt{2}}{2}<\cos \left( x-\frac{\pi }{4} \right)\le 1\Rightarrow 1<t\le \sqrt{2} \).
Do \( t=0\notin \left( 1;\sqrt{2} \right] \) nên ta xét phương trình: \( m(t-1)+1=0 \) (**)
\( \Leftrightarrow mt=m-1\Leftrightarrow t=1-\frac{1}{m} \) (do m = 0 thì (**) vô nghiệm)
Do đó: yêu cầu bài toán \( \Leftrightarrow 1<1-\frac{1}{m}\le \sqrt{2}\Leftrightarrow \left\{ \begin{align} & -\frac{1}{m}>0 \\ & 1-\sqrt{2}\le \frac{1}{m} \\ \end{align} \right. \)
\( \Leftrightarrow \left\{ \begin{align} & m<0 \\ & m\le \frac{1}{1-\sqrt{2}}=-\sqrt{2}-1 \\ \end{align} \right.\Leftrightarrow m\le -\sqrt{2}-1 \).
Câu 12. Cho \( f(x)={{\cos }^{2}}2x+2{{(\sin x+\cos x)}^{3}}-3\sin 2x+m \).
a) Giải phương trình \( f(x)=0 \) khi \( m=-3 \).
b) Tính theo m giá trị lớn nhất và giá trị nhỏ nhất của f(x). Tìm m sao cho \( {{[f(x)]}^{2}}\le 36,\text{ }\forall x\in \mathbb{R} \).
Lời giải:
Đặt \( t=\sin x+\cos x=\sqrt{2}\cos \left( x-\frac{\pi }{4} \right) \) (điều kiện \( \left| t \right|\le \sqrt{2} \))
Thì \( {{t}^{2}}=1+\sin 2x \) và \( {{\cos }^{2}}2x=1-si{{n}^{2}}2x=1-{{({{t}^{2}}-1)}^{2}}=-{{t}^{4}}+2{{t}^{2}} \).
Vậy f(x) thành \( g(t)=-{{t}^{4}}+2{{t}^{2}}+2{{t}^{3}}-3({{t}^{2}}-1)+m \).
a) Khi \( m=-3 \) thì \( g(t)=0 \)
\( \Leftrightarrow -{{t}^{2}}({{t}^{2}}-2t+1)=0\Leftrightarrow \left[ \begin{align} & t=0 \\ & t=1 \\ \end{align} \right. \) \( \Rightarrow \left[ \begin{align} & \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=0 \\ & \sqrt{2}\cos \left( x-\frac{\pi }{4} \right)=1 \\ \end{align} \right. \)
\( \Leftrightarrow \left[ \begin{align} & \cos \left( x-\frac{\pi }{4} \right)=0 \\ & \cos \left( x-\frac{\pi }{4} \right)=\frac{\sqrt{2}}{2}=\cos \frac{\pi }{4} \\ \end{align} \right. \)\(\Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\frac{\pi }{2}+k\pi \\ & x-\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \vee x-\frac{\pi }{4}=-\frac{\pi }{4}+k2\pi \\ \end{align} \right.\)
\(\Leftrightarrow \left[ \begin{align} & x=\frac{3\pi }{4}+k\pi \\ & x=\frac{\pi }{2}+k2\pi \vee x=k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z}\).
b) Ta có: \( {g}'(t)=-4{{t}^{3}}+6{{t}^{2}}-2t=-2t(2{{t}^{2}}-3t+1) \)
Do đó: \( \left\{ \begin{align} & {g}'(t)=0 \\ & t\in \left[ -\sqrt{2};\sqrt{2} \right] \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & t=0 \\ & t=1 \\ & t=\frac{1}{2} \\ \end{align} \right. \).
Ta có: \( g(0)=3+m=g(1),\text{ }g\left( \frac{1}{2} \right)=\frac{47}{16}+m \)
\( g(-\sqrt{2})=4\sqrt{2}-3+m,\text{ }g(\sqrt{2})=m-3-4\sqrt{2} \).
Vậy: \( \underset{x\in \mathbb{R}}{\mathop{max}}\,f(x)=\underset{t\in \left[ -\sqrt{2};\sqrt{2} \right]}{\mathop{max}}\,g(t)=m+3 \).
\( \underset{x\in \mathbb{R}}{\mathop{\min }}\,f(x)=\underset{t\in \left[ -\sqrt{2};\sqrt{2} \right]}{\mathop{\min }}\,g(t)=m-3-4\sqrt{2} \).
Do đó: \( {{[f(x)]}^{2}}\le 36,\text{ }\forall x\in \mathbb{R}\Leftrightarrow -6\le f(x)\le 6,\forall x\in \mathbb{R} \)
\( \Leftrightarrow \left\{ \begin{align} & \underset{\mathbb{R}}{\mathop{max}}\,f(x)\le 6 \\ & \underset{\mathbb{R}}{\mathop{\min }}\,f(x)\ge -6 \\ \end{align} \right. \) \( \Leftrightarrow \left\{ \begin{align} & m+3\le 6 \\ & m-3-4\sqrt{2}\ge -6 \\ \end{align} \right.\Leftrightarrow 4\sqrt{2}-3\le m\le 3 \).