B. Bài tập có lời giải chi tiết (tiếp theo)
Câu 13. Giải phương trình: \( 2\sin x+\cot x=2\sin 2x+1 \) (*)
Lời giải:
Điều kiện: \( \sin x\ne 0\Leftrightarrow \cos x\ne \pm 1 \).
Lúc đó (*) \( \Leftrightarrow 2\sin x+\frac{\cos x}{\sin x}=4\sin x\cos x+1 \)
\( \Leftrightarrow 2{{\sin }^{2}}x+\cos x=4{{\sin }^{2}}x\cos x+\sin x \)
\( \Leftrightarrow 2{{\sin }^{2}}x-\sin x-\cos x(4{{\sin }^{2}}x-1)=0 \)
\( \Leftrightarrow \sin x(2\sin x-1)-\cos x(2\sin x-1)(2\sin x+1)=0 \)
\( \Leftrightarrow (2\sin x-1)\left[ \sin x-\cos x(2\sin x+1) \right]=0 \)
\( \Leftrightarrow \left[ \begin{align} & 2\sin x-1=0\begin{matrix} {} & {} & {} & (1) \\\end{matrix} \\ & \sin x-\cos x-\sin 2x=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right. \)
+ Ta có \( (1)\Leftrightarrow \sin x=\frac{1}{2} \) (nhận do \( \sin x\ne 0 \))
\( \Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{6}+k2\pi \\ & x=\frac{5\pi }{6}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
+ Xét (2): Đặt \( t=\sin x-\cos x=\sqrt{2}\sin \left( x-\frac{\pi }{4} \right) \), với điều kiện \( \left| t \right|\le \sqrt{2} \) và \( t\ne \pm 1 \)
Thì \( {{t}^{2}}=1-\sin 2x \).
Khi đó (2) thành: \( t-(1-{{t}^{2}})=0\Leftrightarrow {{t}^{2}}+t-1=0 \)
\( \Leftrightarrow \left[ \begin{align} & t=\frac{-1+\sqrt{5}}{2}\text{ }(n) \\ & t=\frac{-1-\sqrt{5}}{2}\text{ }(\ell ) \\ \end{align} \right. \)
Do đó: \( \sqrt{2}\sin \left( x-\frac{\pi }{4} \right)=\frac{-1+\sqrt{5}}{2}\Leftrightarrow \sin \left( x-\frac{\pi }{4} \right)=\frac{-1+\sqrt{5}}{2\sqrt{2}} \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\arcsin \left( \frac{\sqrt{5}-1}{2\sqrt{2}} \right)+k2\pi \\ & x-\frac{\pi }{4}=\pi -\arcsin \left( \frac{\sqrt{5}-1}{2\sqrt{2}} \right)+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{4}+\arcsin \left( \frac{\sqrt{5}-1}{2\sqrt{2}} \right)+k2\pi \\ & x=\frac{5\pi }{4}-\arcsin \left( \frac{\sqrt{5}-1}{2\sqrt{2}} \right)+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
Câu 14. Giải phương trình: \( \cos 2x+5=2(2-\cos x)(\sin x-\cos x) \) (*)
Lời giải:
Ta có: (*) \( \Leftrightarrow ({{\cos }^{2}}x-{{\sin }^{2}}x)+5=2(2-\cos x)(\sin x-\cos x) \)
\( \Leftrightarrow (\sin x-\cos x)\left[ 2(2-\cos x)+(\sin x+\cos x) \right]-5=0 \)
\( \Leftrightarrow (\sin x-\cos x)(\sin x-\cos x+4)-5=0 \) (**)
Đặt \( t=\sin x-\cos x=\sqrt{2}\sin \left( x-\frac{\pi }{4} \right) \) với điều kiện \( \left| t \right|\le 2 \).
(**) thành: \( t(t+4)-5=0\Leftrightarrow {{t}^{2}}+4t-5=0\Leftrightarrow \left[ \begin{align} & t=1\text{ }(n) \\ & t=-5\text{ }(\ell ) \\ \end{align} \right. \).
\( \Rightarrow \sqrt{2}\sin \left( x-\frac{\pi }{4} \right)=1\Leftrightarrow \sin \left( x-\frac{\pi }{4} \right)=\frac{\sqrt{2}}{2}=\sin \frac{\pi }{4} \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \\ & x-\frac{\pi }{4}=\pi -\frac{\pi }{4}+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=\frac{\pi }{2}+k2\pi \\ & x=\pi +k2\pi \\ \end{align} \right.,k\in \mathbb{Z} \).
Câu 15. Giải phương trình: \( {{\cos }^{3}}x+{{\sin }^{2}}x=\cos 2x \) (*)
Lời giải:
Ta có: (*) \( \Leftrightarrow (\cos x+\sin x)(1-\sin x\cos x)={{\cos }^{2}}x-{{\sin }^{2}}x \)
\( \Leftrightarrow (\sin x+\cos x)\left[ 1-\sin x\cos x-(\cos x-\sin x) \right]=0 \)
\(\Leftrightarrow \left[ \begin{align} & \sin x+\cos x=0\begin{matrix} {} & {} & {} & (1) \\\end{matrix} \\ & \sin x-\cos x-\sin x\cos x+1=0\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right.\)
+ Giải \( (1)\Leftrightarrow \tan x=-1\Leftrightarrow x=-\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
+ Giải (2): Đặt \( t=\sin x-\cos x=\sqrt{2}\sin \left( x-\frac{\pi }{4} \right)\) với điều kiện \( \left| t \right|\le \sqrt{2} \)
Thì \( {{t}^{2}}=-1-2\sin x\cos x \).
(2) thành: \( t-\frac{1-{{t}^{2}}}{2}+1=0\Leftrightarrow {{t}^{2}}+2t+1=0\Leftrightarrow t=-1 \)
\( \Rightarrow \sqrt{2}\sin \left( x-\frac{\pi }{4} \right)=-1\Leftrightarrow \sin \left( x-\frac{\pi }{4} \right)=-\frac{\sqrt{2}}{2}=\sin \left( -\frac{\pi }{4} \right) \)
\( \Leftrightarrow \left[ \begin{align} & x-\frac{\pi }{4}=-\frac{\pi }{4}+k2\pi \\ & x-\frac{\pi }{4}=\pi +\frac{\pi }{4}+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=k2\pi \\ & x=\frac{3\pi }{2}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
Câu 16. Cho phương trình: \( {{\cos }^{3}}x-{{\sin }^{3}}x=m \) (1)
a) Giải phương trình (1) khi m = 1 bằng cách đặt ẩn phụ \( t=\cos x-\sin x \).
b) Tìm m sao cho (1) có đúng hai nghiệm trên \( \left[ -\frac{\pi }{4};\frac{\pi }{4} \right] \).
Lời giải:
Ta có: \( (1)\Leftrightarrow (\cos x-\sin x)(1+\sin x\cos x)=m \).
Đặt \( t=\cos x-\sin x=\sqrt{2}\cos \left( x+\frac{\pi }{4} \right) \), với điều kiện \( \left| t \right|\le \sqrt{2} \).
Thì \( {{t}^{2}}=1-2\sin x\cos x \).
Khi đó (1) thành: \( t\left( 1+\frac{1-{{t}^{2}}}{2} \right)=m\Leftrightarrow t(3-{{t}^{2}})=2m \) (2)
a) Khi \( m=1 \) thì (2) thành: \( {{t}^{3}}-3t+2=0\Leftrightarrow (t-1)({{t}^{2}}+t-2)=0 \)
\( \Leftrightarrow \left[ \begin{align} & t=1\text{ }(n) \\ & t=-2\text{ }(\ell ) \\ \end{align} \right. \).
Suy ra: \( \sqrt{2}\cos \left( x+\frac{\pi }{4} \right)=1\Leftrightarrow \cos \left( x+\frac{\pi }{4} \right)=\frac{\sqrt{2}}{2}=\cos \frac{\pi }{4} \)
\( \Leftrightarrow \left[ \begin{align} & x+\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \\ & x+\frac{\pi }{4}=-\frac{\pi }{4}+k2\pi \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=k2\pi \\ & x=-\frac{\pi }{2}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z} \).
b) Nếu \( x\in \left[ -\frac{\pi }{4};\frac{\pi }{4} \right] \) thì \( 0\le x+\frac{\pi }{4}\le \frac{\pi }{2} \) nên \( 0\le \cos \left( x+\frac{\pi }{4} \right)\le 1 \)
\( \Leftrightarrow 0\le t=\sqrt{2}\cos \left( x+\frac{\pi }{4} \right)\le \sqrt{2} \)
Nhận xét rằng với mỗi t tìm được trên \( \left[ 0;\sqrt{2} \right] \).
Ta tìm duy nhất một \( x\in \left[ -\frac{\pi }{4};\frac{\pi }{4} \right] \).
Xét \( f(t)=-{{t}^{3}}+3t \) trên \( \left[ 0;\sqrt{2} \right] \).
\( \Rightarrow {f}'(t)=-3{{t}^{2}}+3 \).
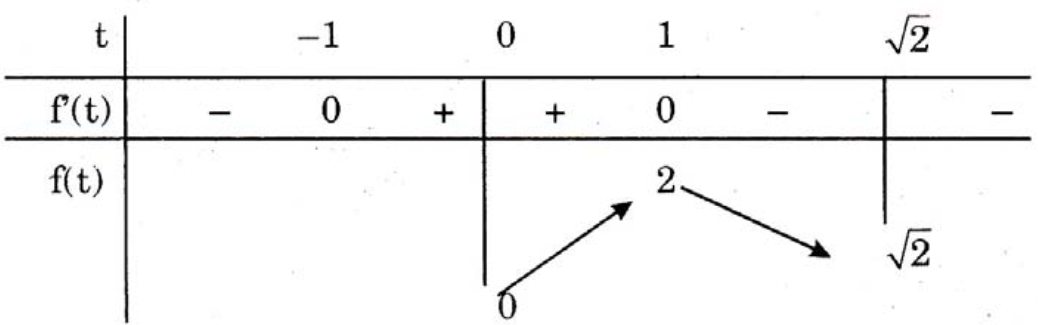
Vậy (1) có đúng hai nghiệm \( x\in \left[ -\frac{\pi }{4};\frac{\pi }{4} \right] \)
\( \Leftrightarrow (d):y=2m \) cắt \( (C):y=-{{t}^{3}}+3t \) trên \( \left[ 0;\sqrt{2} \right] \) tại 2 điểm phân biệt
\( \Leftrightarrow \sqrt{2}\le 2m<2\Leftrightarrow \frac{\sqrt{2}}{2}\le m<1 \).
Câu 17. Cho phương trình: \( 2\cos 2x+{{\sin }^{2}}xcosx+sinxco{{s}^{2}}x=m(\sin x+\cos x) \) (*)
a) Giải phương trình khi \( m=2 \).
b) Tìm m để phương trình (*) có ít nhất một nghiệm trên \( \left[ 0;\frac{\pi }{2} \right] \).
Lời giải:
Ta có: (*) \( \Leftrightarrow 2({{\cos }^{2}}x-{{\sin }^{2}}x)+\sin x\cos x(\sin x+\cos x)=m(\sin x+\cos x) \)
\( \Leftrightarrow (\cos x+\sin x)\left[ 2(\cos x-\sin x)+\sin x\cos x-m \right]=0 \)
\( \Leftrightarrow \left[ \begin{align} & \cos x+\sin x=0\begin{matrix} {} & {} & {} & (1) \\\end{matrix} \\ & 2(\cos x-\sin x)+\sin x\cos x=m\begin{matrix} {} & (2) \\\end{matrix} \\ \end{align} \right. \).
Đặt \( t=\cos x-\sin x=\sqrt{2}\cos \left( x+\frac{\pi }{4} \right) \), với điều kiện \( \left| t \right|\le \sqrt{2} \).
Thì \( {{t}^{2}}=1-2\sin x\cos x \).
Ta có: \( (1)\Leftrightarrow \sin x=-\cos x\Leftrightarrow \tan x=-1\Leftrightarrow x=-\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Phương trình (2) thành: \( 2t+\frac{1-{{t}^{2}}}{2}=m\Leftrightarrow -{{t}^{2}}+4t+1=2m \) (**)
a) Khi \( m=2 \) thì (**) thành: \( {{t}^{2}}-4t+3=0\Leftrightarrow \left[ \begin{align} & t=1\text{ }(n) \\ & t=3\text{ }(\ell ) \\ \end{align} \right. \).
Khi đó: \(\sqrt{2}\cos \left( x+\frac{\pi }{4} \right)=1\Leftrightarrow \cos \left( x+\frac{\pi }{4} \right)=\frac{\sqrt{2}}{2}=\cos \frac{\pi }{4}\)
\(\Leftrightarrow \left[ \begin{align} & x+\frac{\pi }{4}=\frac{\pi }{4}+k2\pi \\ & x+\frac{\pi }{4}=-\frac{\pi }{4}+k2\pi \\ \end{align} \right.\)\(\Leftrightarrow \left[ \begin{align} & x=k2\pi \\ & x=-\frac{\pi }{2}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z}\).
Vậy nghiệm của phương trình là: \(\left[ \begin{align} & x=-\frac{\pi }{4}+k\pi \\ & x=k2\pi \\ & x=-\frac{\pi }{2}+k2\pi \\ \end{align} \right.,\text{ }k\in \mathbb{Z}\).
b) Ta có: \( x\in \left[ 0;\frac{\pi }{2} \right]\Leftrightarrow x+\frac{\pi }{4}\in \left[ \frac{\pi }{4};\frac{3\pi }{4} \right] \).
\(\Rightarrow -\frac{\sqrt{2}}{2}\le \cos \left( x+\frac{\pi }{4} \right)\le \frac{\sqrt{2}}{2}\Rightarrow -1\le t\le 1\).
Do nghiệm \( x=-\frac{\pi }{4}+k\pi \notin \left[ 0;\frac{\pi }{2} \right],\text{ }\forall k\in \mathbb{R} \).
Nên yêu cầu bài toán \( \Leftrightarrow \) (**) có nghiệm trên \( [-1;1] \).
Xét \( y=-{{t}^{2}}+4t+1 \) thì \( {y}’=-2t+4>0,\forall t\in [-1;1] \).
\( \Rightarrow y \) đồng biến trên \( [-1;1] \).
Do đó: yêu cầu bài toán \( \Leftrightarrow -4=y(-1)\le 2m\le y(1)=4\Leftrightarrow -2\le m\le 2 \).
Câu 18. Giải phương trình: \( 3{{\tan }^{2}}x+4\tan x+4\cot x+3{{\cot }^{2}}x+2=0 \) (*)
Lời giải:
Đặt \( t=\tan x+\cot x=\frac{2}{\sin 2x} \), với điều kiện \( \left| t \right|\ge 2 \).
Thì \( {{t}^{2}}={{\tan }^{2}}x+{{\cot }^{2}}x+2 \).
(*) thành: \( 3({{t}^{2}}-2)+4t+2=0\Leftrightarrow 3{{t}^{2}}+4t-4=0\Leftrightarrow \left[ \begin{align} & t=\frac{2}{3}\text{ }(\ell ) \\ & t=-2\text{ }(n) \\ \end{align} \right. \).
Với \( t=-2\Leftrightarrow \frac{2}{\sin 2x}=-2\Leftrightarrow \sin 2x=-1\Leftrightarrow 2x=-\frac{\pi }{2}+k2\pi \)
\( \Leftrightarrow x=-\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Câu 19. Giải phương trình: \( \tan x+{{\tan }^{2}}x+{{\tan }^{3}}x+\cot x+{{\cot }^{2}}x+{{\cot }^{3}}x=6 \) (*)
Lời giải:
Ta có: (*) \( \Leftrightarrow (\tan x+\cot x)+({{\tan }^{2}}x+{{\cot }^{2}}x)+({{\tan }^{3}}x+{{\cot }^{3}}x)=6 \)
\( \Leftrightarrow (\tan x+\cot x)+{{(\tan x+\cot x)}^{2}}-2+(\tan x+\cot x)({{\tan }^{2}}x+{{\cot }^{2}}x-1)=6 \)
\( \Leftrightarrow (\tan x+\cot x)+{{(\tan x+\cot x)}^{2}}+(\tan x+\cot x)\left[ {{(\tan x+\cot x)}^{2}}-3 \right]=8 \) (**)
Đặt \( t=\tan x+\cot x=\frac{2}{\sin 2x} \), với điều kiện \( \left| t \right|\ge 2 \).
Khi đó phương trình (**) thành: \( t+{{t}^{2}}+t({{t}^{2}}-3)=8\Leftrightarrow {{t}^{3}}+{{t}^{2}}-2t-8=0 \)
\(\Leftrightarrow (t-2)({{t}^{2}}+3t+4)=0\Leftrightarrow \left[ \begin{align} & t=2\text{ }(n) \\ & {{t}^{2}}+3t+4=0\text{ }(\text{vô nghiệm }) \\ \end{align} \right.\)
Với \( t=2\Rightarrow \frac{2}{\sin 2x}=2\Leftrightarrow \sin 2x=1 \)
\( \Leftrightarrow 2x=\frac{\pi }{2}+k2\pi \Leftrightarrow x=\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Câu 20. Giải phương trình: \( \frac{2}{{{\sin }^{2}}x}+2{{\tan }^{2}}x+5\tan x+5\cot x+4=0 \) (*)
Lời giải:
Cách 1: (*) \( \Leftrightarrow 2(1+{{\cot }^{2}}x)+2{{\tan }^{2}}x+5(\tan x+\cot x)+4=0 \)
\( \Leftrightarrow 2({{\tan }^{2}}x+{{\cot }^{2}}x)+5(\tan x+\cot x)+6=0 \)
\( \Leftrightarrow 2\left[ {{(\tan x+\cot x)}^{2}}-2 \right]+5(\tan x+\cot x)+6=0 \).
Đặt \( t=\tan x+\cot x=\frac{2}{\sin 2x} \), với điều kiện \( \left| t \right|\ge 2 \).
Ta được phương trình: \( 2{{t}^{2}}+5t+2=0\Leftrightarrow \left[ \begin{align} & t=-2\text{ }(n) \\ & t=-\frac{1}{2}\text{ }(\ell ) \\ \end{align} \right. \).
Với \( t=-2\Rightarrow \frac{2}{\sin 2x}=-2\Leftrightarrow \sin 2x=-1 \)
\( \Leftrightarrow 2x=-\frac{\pi }{2}+k2\pi \Leftrightarrow x=-\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Cách 2: Đặt \( u=\tan x \) (với điều kiện \( u\ne 0 \)).
Phương trình (*) thành: \( 2+\frac{2}{{{u}^{2}}}+2{{u}^{2}}+5u+\frac{5}{u}+4=0 \)
\( \Leftrightarrow 2+2{{u}^{4}}+5{{u}^{3}}+5u+6{{u}^{2}}=0\Leftrightarrow (u+1)(2{{u}^{3}}+3{{u}^{2}}+3u+2)=0 \)
\(\Leftrightarrow {{(u+1)}^{2}}(2{{u}^{2}}+u+2)=0\Leftrightarrow \left[ \begin{align} & u=-1\text{ }(n) \\ & 2{{u}^{2}}+u+2=0\text{ }(\text{vô nghiệm }) \\ \end{align} \right.\)
Với \( u=-1\Rightarrow \tan x=-1\Leftrightarrow x=-\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
Câu 21. Cho phương trình: \( \frac{1}{{{\cos }^{2}}x}+{{\cot }^{2}}x+m(\tan x+\cot x)+2=0 \) (1)
a) Giải phương trình khi \( m=\frac{5}{2} \).
b) Tìm m để phương trình có nghiệm.
Lời giải:
Ta có: \( (1)\Leftrightarrow {{\tan }^{2}}x+co{{t}^{2}}x+m(tanx+cotx)+3=0 \)
Đặt \( t=\tan x+\cot x=\frac{2}{\sin 2x} \) (điều kiện \( \left| t \right|\ge 2 \))
\( \Rightarrow {{t}^{2}}={{\tan }^{2}}x+{{\cot }^{2}}x+2 \)
Phương trình (1) thành: \( {{t}^{2}}+mt+1=0 \) (2)
a) Khi \( m=\frac{5}{2} \) ta được phương trình: \( 2{{t}^{2}}+5t+2=0 \)
\( \Leftrightarrow \left[ \begin{align} & t=-2\text{ }(n) \\ & t=-\frac{1}{2}\text{ }(\ell ) \\ \end{align} \right. \).
Suy ra: \( \frac{2}{\sin 2x}=-2\Leftrightarrow \sin 2x=-1 \)
\( \Leftrightarrow 2x=-\frac{\pi }{2}+k2\pi \Leftrightarrow x=-\frac{\pi }{4}+k\pi ,\text{ }k\in \mathbb{Z} \).
b)
Ta có: \( (2)\Leftrightarrow mt=-1-{{t}^{2}}\Leftrightarrow m=-\frac{1}{t}-t \) (do \( t=0 \) không là nghiệm của (2))
Xét \( y=-\frac{1}{t}-t \) với \( \left| t \right|\ge 2 \).
Thì \( {y}’=\frac{1}{{{t}^{2}}}-1=\frac{1-{{t}^{2}}}{{{t}^{2}}} \).
Ta có: \( {y}’=0\Leftrightarrow t=\pm 1 \).
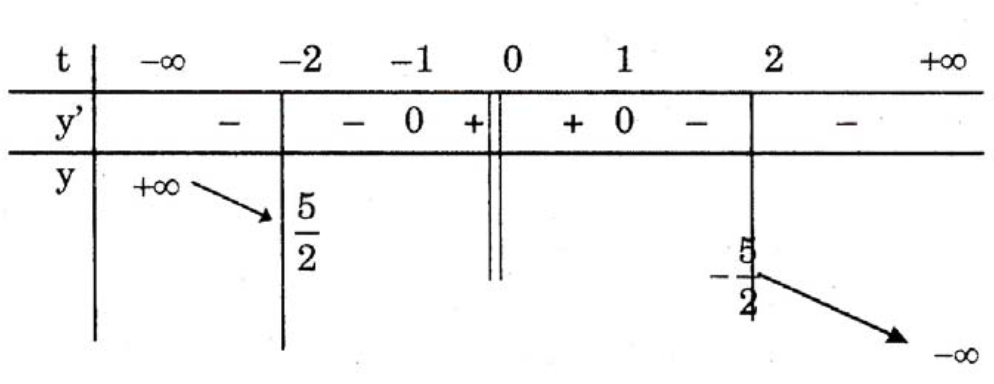
Do đó (1) có nghiệm \( \Leftrightarrow (d):y=m \) cắt \( (C):y=-\frac{1}{t}-t \) trên \( \left( -\infty ;-2 \right]\cup \left[ 2;+\infty \right) \)
\( \Leftrightarrow m\le -\frac{5}{2}\vee m\ge \frac{5}{2} \).