Trung Tâm Luyện Thi Đại Học
Dạng 3. Khối tròn xoay nội, ngoại tiếp khối đa diện
A. Công thức tính Khối tròn xoay nội, ngoại tiếp khối đa diện
Trường hợp
B. Bài tập có hướng dẫn giải
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng HSG Toán Lý Hóa các lớp - Ôn thi vào lớp 10 Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
Câu 1. (THPTQG – 123 – 2017) Trong hình chóp tứ giác đều S.ABCD có cạnh đều bằng \( a\sqrt{2} \). Tính thể tích V của khối nón đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD.
A. \( V=\frac{\sqrt{2}\pi {{a}^{3}}}{2} \).
B. \( V=\frac{\pi {{a}^{3}}}{2} \).
C. \( V=\frac{\pi {{a}^{3}}}{6} \).
D. \( V=\frac{\sqrt{2}\pi {{a}^{3}}}{6} \).
Hướng dẫn giải:
Chọn C
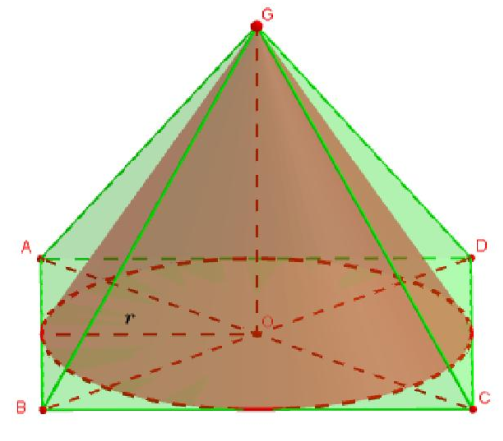
Gọi \( O=AC\cap BD\Rightarrow SO\bot (ABCD) \).
Lại có \( OC=\frac{AC}{2}=a\Rightarrow SO=\sqrt{S{{A}^{2}}-O{{C}^{2}}}=a \).
Bán kính \( r=\frac{AB}{2}=\frac{a}{\sqrt{2}} \).
Suy ra thể tích khối nón là \( V=\frac{1}{3}\pi {{\left( \frac{a}{\sqrt{2}} \right)}^{2}}.a=\frac{\pi {{a}^{3}}}{6} \).
Câu 2. (THPTQG – 110 – 2017) Cho tứ diện đều ABCD có cạnh bằng 3a. Hình nón (N) có đỉnh A có đáy là đường tròn ngoại tiếp tam giác BCD. Tính diện tích xung quanh \( {{S}_{xq}} \) của (N).
A. \( {{S}_{xq}}=12\pi {{a}^{2}} \).
B. \( {{S}_{xq}}=6\pi {{a}^{2}} \).
C. \( {{S}_{xq}}=3\sqrt{3}\pi {{a}^{2}} \).
D. \( {{S}_{xq}}=16\sqrt{3}\pi {{a}^{2}} \).
Hướng dẫn giải:
Chọn C
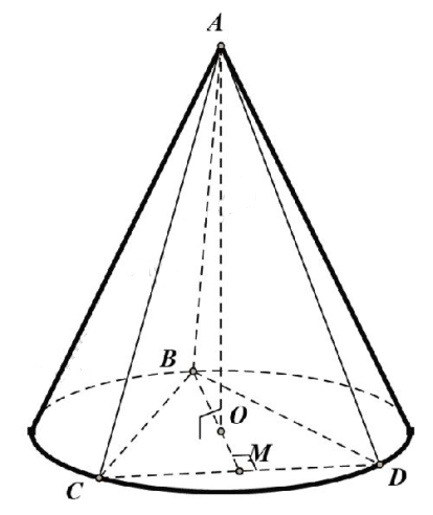
Gọi r là bán kính đường tròn ngoại tiếp tam giác BCD.
Ta có: \( BM=\frac{3a\sqrt{3}}{2};\,\,r=\frac{2}{3}BM=\frac{2}{3}.\frac{3a\sqrt{3}}{2}=a\sqrt{3} \).
\( {{S}_{xq}}=\pi .r.\ell =\pi .r.AB=\pi .a\sqrt{3}.3a=3\sqrt{3}\pi {{a}^{2}} \).
Câu 3. (Chuyên ĐHSP Hà Nội – 2018) Cho hình chóp tam giác đều S.ABC. Hình nón có đỉnh S và có đường tròn đáy là đường tròn nội tiếp tam giác ABC gọi là hình nón nội tiếp hình chóp S.ABC, hình nón có đỉnh S và có đường tròn đáy là đường tròn ngoại tiếp tam giác ABC gọi là hình nón ngoại tiếp hình chóp S.ABC. Tỉ số thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp đã cho là:
A. \( \frac{1}{2} \).
B. \( \frac{1}{4} \).
C. \( \frac{2}{3} \).
D. \( \frac{1}{3} \).
Hướng dẫn giải:
Chọn B
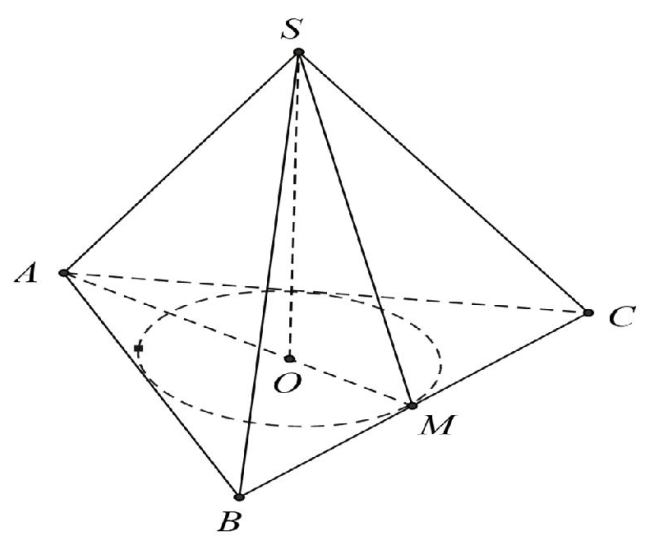
Gọi M là trung điểm của BC.
Gọi O là trọng tâm của tam giác ABC.
Ta có: \( SO\bot (ABC) \) tại O. Suy ra, O là tâm đường tròn nội tiếp và cũng là tâm của đường tròn ngoại tiếp tam giác ABC.
Gọi a là độ dài cạnh của tam giác aBC.
Gọi \( {{V}_{1}},\,\,{{V}_{2}} \) lần lượt là thể tích của hình nón nội tiếp và hình nón ngoại tiếp hình chóp S.ABC.
Do \( OM=\frac{1}{2}OA \) nên ta có:
\( \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\frac{1}{3}.\pi .O{{M}^{2}}.SO}{\frac{1}{3}.\pi .O{{A}^{2}}.SO}=\frac{O{{M}^{2}}}{O{{A}^{2}}}={{\left( \frac{OM}{OA} \right)}^{2}}=\frac{1}{4} \).
Câu 4. (Hồng Bàng – Hải Phòng – 2018) Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng \( 60{}^\circ \). Diện tích xung quanh của hình nón đỉnh S, có đáy là hình tròn ngoại tiếp tam giác ABC bằng
A. \( \frac{\pi {{a}^{2}}\sqrt{10}}{8} \).
B. \( \frac{\pi {{a}^{2}}\sqrt{3}}{3} \).
C. \( \frac{\pi {{a}^{2}}\sqrt{7}}{4} \).
D. \( \frac{\pi {{a}^{2}}\sqrt{7}}{6} \).
Hướng dẫn giải:
Chọn D
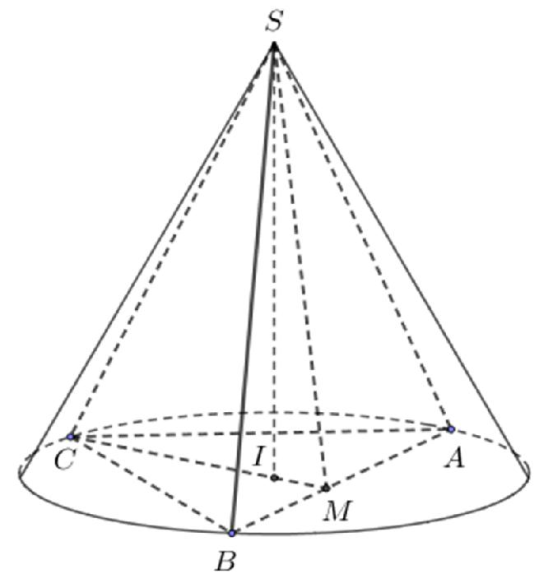
Gọi I là tâm đường tròn (ABC) \( \Rightarrow IA=r=\frac{a\sqrt{3}}{3} \).
Gọi M là trung điểm của AB \( \Rightarrow AB\bot (SMC) \).
\( \Rightarrow \) Góc giữa mặt bên và mặt đáy là góc \( \widehat{SMC}=60{}^\circ \) \( \Rightarrow SM=2IM=\frac{2a\sqrt{3}}{6}=\frac{a\sqrt{3}}{3} \).
\( \Rightarrow SA=\sqrt{S{{M}^{2}}+M{{A}^{2}}}=\sqrt{\frac{{{a}^{2}}}{3}+\frac{{{a}^{2}}}{4}}=\frac{a\sqrt{21}}{6} \).
Diện tích xung quanh hình nón \( {{S}_{xq}}=\pi r\ell =\pi .\frac{a\sqrt{3}}{3}.\frac{a\sqrt{21}}{6}=\frac{\pi {{a}^{2}}\sqrt{7}}{6} \).
Câu 5. Cho hình lập phương ABCD.A’B’C’D’ có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nôi tiếp hình vuông \( A’B’C’D’ \). Diện tích toàn phần của khối nón đó là:
A. \( {{S}_{tp}}=\frac{\pi {{a}^{2}}}{2}\left( \sqrt{3}+2 \right) \).
B. \( {{S}_{tp}}=\frac{\pi {{a}^{2}}}{4}\left( \sqrt{5}+1 \right) \).
C. \( {{S}_{tp}}=\frac{\pi {{a}^{2}}}{4}\left( \sqrt{5}+2 \right) \).
D. \( {{S}_{tp}}=\frac{\pi {{a}^{2}}}{2}\left( \sqrt{3}+1 \right) \).
Hướng dẫn giải:
Chọn B
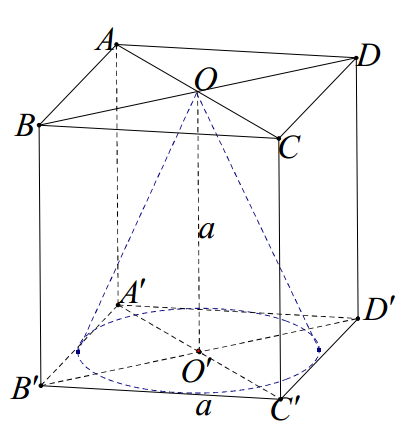
Bán kính của đường tròn đáy là \( r=\frac{a}{2} \).
Diện tích đáy nón là: \( {{S}_{1}}=\pi {{r}^{2}}=\frac{\pi {{a}^{2}}}{4} \).
Độ dài đường sinh là: \( \ell =\sqrt{{{a}^{2}}+{{r}^{2}}}=\frac{a\sqrt{5}}{2} \).
Diện tích xung quanh của khối nón là: \( {{S}_{2}}=\pi r\ell =\frac{\pi {{a}^{2}}\sqrt{5}}{4} \).
Vậy, diện tích toàn phần của khối nón đó là: \( {{S}_{tp}}={{S}_{1}}+{{S}_{2}}=\frac{\pi {{a}^{2}}}{4}\left( \sqrt{5}+1 \right) \).
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng HSG Toán Lý Hóa các lớp - Ôn thi vào lớp 10 Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
Câu 6. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng \( 60{}^\circ \) . Tính diện tích xung quanh của hình nón đỉnh S, đáy là hình tròn ngoại tiếp tam giác ABC.
A. \( \frac{\pi {{a}^{2}}\sqrt{3}}{3} \).
B. \( \frac{\pi {{a}^{2}}\sqrt{7}}{6} \).
C. \( \frac{\pi {{a}^{2}}\sqrt{7}}{4} \).
D. \( \frac{\pi {{a}^{2}}\sqrt{10}}{8} \).
Hướng dẫn giải:
Chọn B
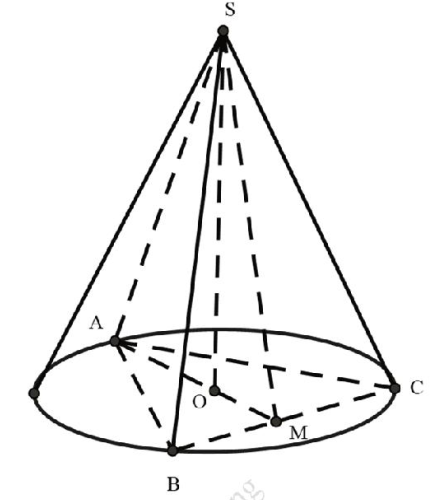
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, M là trung điểm cạnh BC, ta có: \( OM=\frac{a\sqrt{3}}{6},\,\,OA=\frac{a\sqrt{3}}{3} \) và \( \widehat{SMO}=60{}^\circ \) .
Trong tam giác vuông SMO, ta có: \( SO=OM.\tan 60{}^\circ =\frac{a\sqrt{3}}{6}.\sqrt{3}=\frac{a}{2}\Rightarrow SA=\sqrt{\frac{{{a}^{2}}}{4}+\frac{{{a}^{2}}}{3}}=\frac{a\sqrt{7}}{2\sqrt{3}} \).
Vậy \( {{S}_{xq}}=\pi .OA.SA=\pi .\frac{a\sqrt{3}}{3}.\frac{a\sqrt{7}}{2\sqrt{3}}=\frac{\pi {{a}^{2}}\sqrt{7}}{6} \).
Câu 7. Cho hình nón (N) có đường sinh tạo với đáy một góc \( 60{}^\circ \) . Mặt phẳng qua trục của (N) cắt (N) được thiết diện là một tam giác có bán kính đường tròn nội tiếp bằng 1. Tính thể tích V của khối nón giới hạn bởi (N).
A. \( V=9\pi \).
B. \( V=3\sqrt{3}\pi \).
C. \( V=9\sqrt{3}\pi \).
D. \( V=3\pi \).
Hướng dẫn giải:
Chọn D
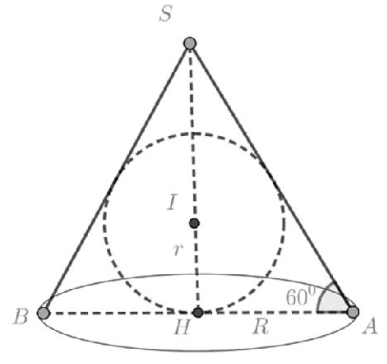
Hình nón (N) có đường sinh tạo với đáy một góc \( 60{}^\circ \) nên \( \widehat{SAH}=60{}^\circ \) .
Ta có \( \Delta SAB \) cân tại S có \( \widehat{A}=60{}^\circ \) nên \( \Delta SAB \) đều. Do đó tâm I của đường tròn nội tiếp \( \Delta SAB \) cũng là trọng tâm của \( \Delta SAB \).
Suy ra \( SH=3IH=3 \).
Mặt khác \( SH=\frac{AB\sqrt{3}}{2}\Rightarrow AB=2\sqrt{3}\Rightarrow R=\sqrt{3}\Rightarrow {{S}_{\text{}}}=\pi {{R}^{2}}=3\pi \).
Do đó: \( V=\frac{1}{3}SH.{{S}_{\text{}}}=\frac{1}{3}.3.3\pi =3\pi \) .
Câu 8. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và mặt đáy bằng \( 60{}^\circ \) . Tính diện tích xung quanh của hình nón đỉnh S, đáy là hình tròn ngoại tiếp tam giác ABC.
A. \( \frac{\pi {{a}^{2}}\sqrt{3}}{3} \).
B. \( \frac{\pi {{a}^{2}}\sqrt{7}}{6} \).
C. \( \frac{\pi {{a}^{2}}\sqrt{7}}{4} \).
D. \( \frac{\pi {{a}^{2}}\sqrt{10}}{8} \).
Hướng dẫn giải:
Chọn B
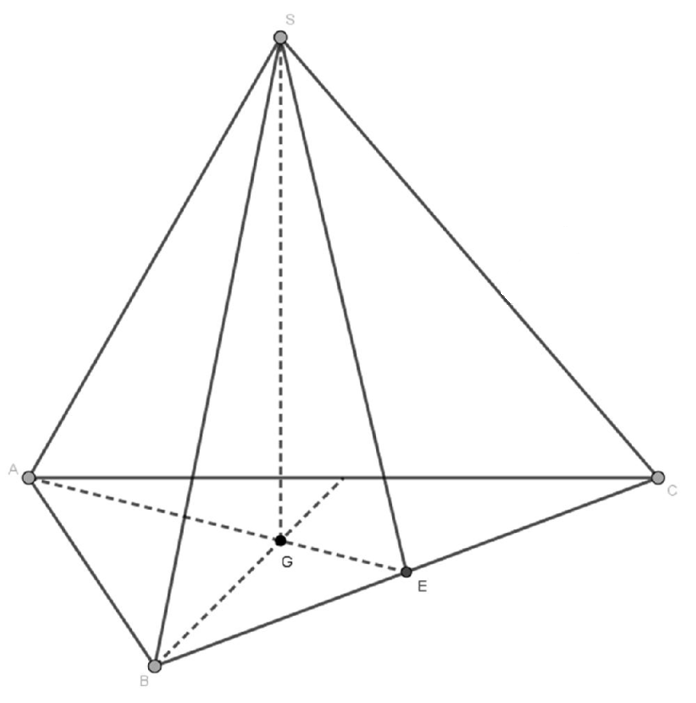
Gọi E là trung điểm BC. Theo giả thiết \( \widehat{SEA}=60{}^\circ \).
Suy ra \( : SA=\frac{a\sqrt{7}}{2\sqrt{3}}=\ell \) .
\( {{S}_{xq}}=\pi R\ell =\pi .\frac{a\sqrt{3}}{3}.\frac{a\sqrt{7}}{2\sqrt{3}}=\frac{\pi {{a}^{2}}\sqrt{7}}{6} \).
Câu 9. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy là a và (N) là hình nón có đỉnh là S với đáy là đường tròn ngoại tiếp tứ giác ABCD. Tỉ số thể tích của khối chóp S.ABCD và khối nón (N) là:
A. \( \frac{\pi }{4} \).
B. \( \frac{\pi \sqrt{2}}{2} \).
C. \( \frac{2}{\pi } \).
D. \( \frac{2\sqrt{2}}{\pi } \).
Hướng dẫn giải:
Chọn C
Gọi h là chiều cao của khối chóp và đồng thời là đường cao của khối nón.
Thể tích của khối chóp là \( {{V}_{1}}=\frac{1}{3}{{a}^{2}}h \).
Bán kính của đường tròn ngoại tiếp đáy ABCD là \( r=\frac{AC}{2}=\frac{a\sqrt{2}}{2} \).
Thể tích của khối nón là \( {{V}_{2}}=\frac{1}{3}\pi .\frac{{{a}^{2}}}{2}.h \).
Tỉ số thể tích của khối chóp S.ABCD và khối nón (N) là \( \frac{{{V}_{1}}}{{{V}_{2}}}=\frac{2}{\pi } \).
Câu 10. Cho hình chóp đều S.ABCD có đáy là hình vuông cạnh 2a, cạnh bên tạo với đáy góc \( 45{}^\circ \). Thể tích khối nón ngoại tiếp hình chóp trên là:
A. \( \frac{8\sqrt{3}}{3}\pi {{a}^{3}} \).
B. \( \frac{2\sqrt{3}}{3}\pi {{a}^{3}} \).
C. \( 2\sqrt{2}\pi {{a}^{3}} \).
D. \( \frac{2}{3}\pi {{a}^{3}} \).
Hướng dẫn giải:
Chọn D
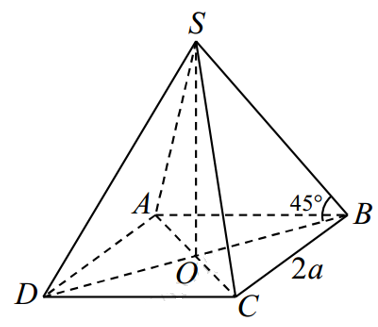
Ta có S.ABCD là hình chóp đều, gọi \( O=AC\cap BD \).
\( \Rightarrow \) Góc giữa cạnh bên với mặt đáy là \( \widehat{SBO}=45{}^\circ \) .
ABCD là hình vuông cạnh 2a \( \Rightarrow BD=2\sqrt{2}a \).
Khối nón ngoại tiếp hình chóp S.ABCD có bán kính đường tròn đáy \( R=\frac{BD}{2}=a\sqrt{2} \).
\( \Delta SOB \) vuông cân tại O.
\( \Rightarrow \) Chiều cao khối nón \( h=SO=OB=\sqrt{2}a \).
\( \Rightarrow \) Thể tích khối nón là: \( V=\frac{1}{3}\pi {{R}^{2}}h=\frac{1}{3}\pi {{\left( a\sqrt{2} \right)}^{2}}.a\sqrt{2}=\frac{2\sqrt{2}}{3}\pi {{a}^{3}} \).
Câu 11. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Tam giác SAB có diện tích bằng \( 2{{a}^{2}} \). Thể tích của khối nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD.
A. \( \frac{\pi {{a}^{3}}\sqrt{7}}{8} \).
B. \( \frac{\pi {{a}^{3}}\sqrt{7}}{7} \).
C. \( \frac{\pi {{a}^{3}}\sqrt{7}}{4} \).
D. \( \frac{\pi {{a}^{3}}\sqrt{15}}{24} \).
Hướng dẫn giải:
Chọn A
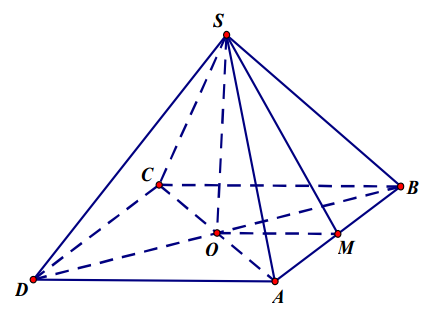
Gọi \( O=AC\cap BD \) và M là trung điểm AB. Hình nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD có bán kính đáy là \( R=OM=\frac{a}{2} \) và có chiều cao là \( h=SO \).
Thể tích khối nón \( V=\frac{1}{3}B.h \) trong đó \( B=\pi {{R}^{2}}=\frac{\pi {{a}^{2}}}{4} \).
Diện tích tam giác SAB là \( 2{{a}^{2}} \) nên \(\frac{\text{1}}{\text{2}}SM.AB=2{{a}^{2}}\Leftrightarrow SM=4a\).
Trong tam giác vuông SOM, ta có \( SO=\sqrt{S{{M}^{2}}-O{{M}^{2}}}=\sqrt{16{{a}^{2}}-\frac{{{a}^{2}}}{4}}=\frac{3a\sqrt{7}}{2}=h \).
Vậy thể tích của khối nón là \( V=\frac{\pi {{a}^{3}}\sqrt{7}}{8} \).
Câu 12. Cho hình lập phương ABCD.A’B’C’D’ có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’. Kết quả tính diện tích toàn phần \( {{S}_{tp}} \) của khối nón đó có dạng bằng \( \frac{\pi {{a}^{2}}}{4}\left( \sqrt{b}+c \right) \) với b và c là hai số nguyên dương và \( b>1 \). Tính \( bc \).
A. \( bc=5 \).
B. \( bc=8 \).
C. \( bc=15 \).
D. \( bc=7 \).
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng HSG Toán Lý Hóa các lớp - Ôn thi vào lớp 10 Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
Hướng dẫn giải:
Chọn A
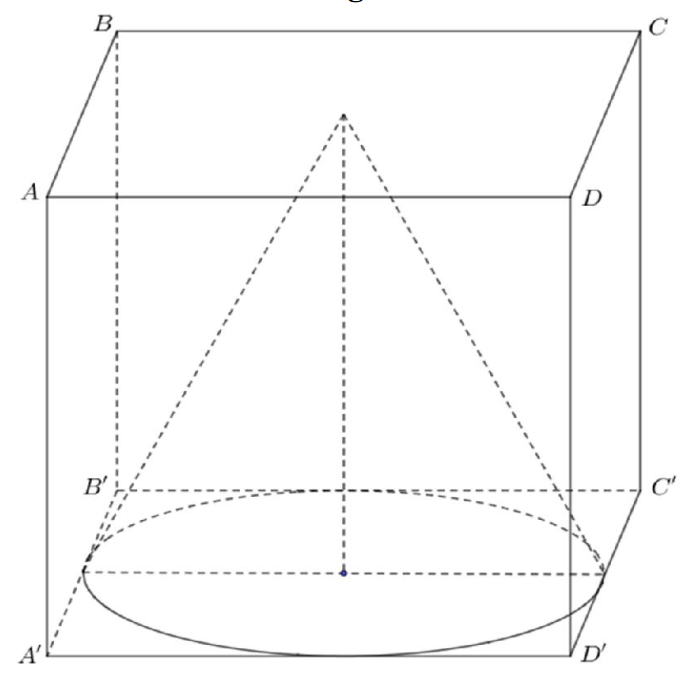
Ta có bán kính hình nón \( r=\frac{a}{2} \), đường cao \( h=a \), đường sinh \( \ell =\frac{a\sqrt{5}}{2} \).
Diện tích toàn phần \( {{S}_{tp}}=\pi r\ell +\pi {{r}^{2}}=\pi \frac{{{a}^{2}}\sqrt{5}}{4}+\pi \frac{{{a}^{2}}}{4}=\frac{\pi {{a}^{2}}}{4}\left( \sqrt{5}+1 \right)\Rightarrow b=5,\,\,c=1 \).
Vậy \( bc=5 \).
Câu 13. Cho hình chóp tam giác đều S.ABC có cạnh \( AB=a \), góc tạo bởi (SAB) và (ABC) bằng \( 60{}^\circ \) . Diện tích xung quanh của hình nón đỉnh S và có đường tròn đáy ngoại tiếp tam giác ABC bằng
A. \( \frac{\sqrt{7}\pi {{a}^{2}}}{3} \).
B. \( \frac{\sqrt{7}\pi {{a}^{2}}}{6} \).
C. \( \frac{\sqrt{3}\pi {{a}^{2}}}{2} \).
D. \( \frac{\sqrt{3}\pi {{a}^{2}}}{6} \).
Hướng dẫn giải:
Chọn B
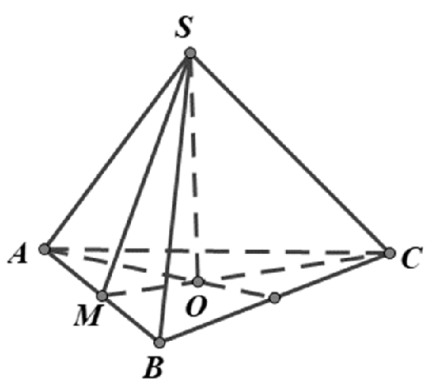
Gọi M là trung điểm AB và gọi O là tâm của tam giác ABC ta có:
\( \left\{ \begin{align} & AB\bot CM \\ & AB\bot SO \\ \end{align} \right.\Rightarrow AB\bot (SCM)\Rightarrow AB\bot SM,\,\,AB\bot CM \).
Do đó \( \left( (SAB),(ABC) \right)=\widehat{SMO}=60{}^\circ \) .
Mặt khác, tam giác ABC đều cạnh a nên \( CM=\frac{a\sqrt{3}}{2} \). Suy ra \( OM=\frac{1}{3}CM=\frac{a\sqrt{3}}{6} \).
\( SO=OM.\tan 60{}^\circ =\frac{a\sqrt{3}}{6}.\sqrt{3}=\frac{a}{2} \).
Hình nón đã cho có chiều cao \( h=SO=\frac{a}{2} \), bán kính đáy \( R=OA=\frac{a\sqrt{3}}{3} \), độ dài đường sinh \( \ell =\sqrt{{{h}^{2}}+{{R}^{2}}}=\frac{a\sqrt{21}}{6} \).
Diện tích xung quanh hình nón là: \( {{S}_{xq}}=\pi .R.\ell =\pi .\frac{a\sqrt{3}}{3}.\frac{a\sqrt{21}}{6}=\frac{\sqrt{7}\pi {{a}^{2}}}{6} \).
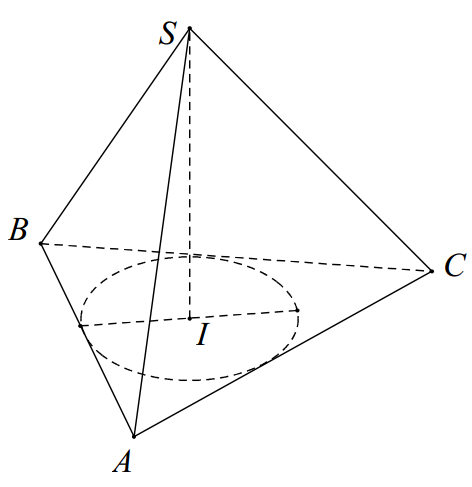
Câu 14. Cho hình nón đỉnh S, đáy là hình tròn nội tiếp tam giác ABC. Biết rằng \( AB=BC=10a \), \( AC=12a \), góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng \( 45{}^\circ \). Tính thể tích V của khối nón đã cho.
A. \( V=3\pi {{a}^{3}} \).
B. \( V=9\pi {{a}^{3}} \).
C. \( V=27\pi {{a}^{3}} \).
D. \( V=12\pi {{a}^{3}} \).
Hướng dẫn giải:
Chọn B
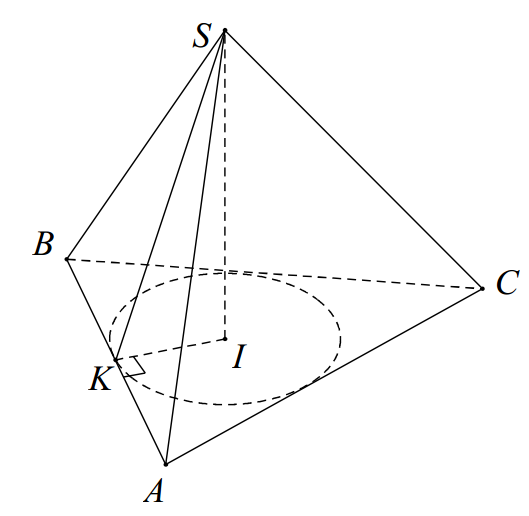
Dựng \( IK\bot AB \), suy ra \( \left( (SAB),(ABC) \right)=\widehat{SKI}=45{}^\circ \) .
Xét \( \Delta ABC \), ta có: \( p=\frac{AB+BC+AC}{2}=\frac{10a+10a+12a}{2}=16a \).
Suy ra: \( {{S}_{\Delta ABC}}=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{16a.6a.6a.4a}=48{{a}^{2}} \).
Bán kính đường tròn nội tiếp là \( r=\frac{S}{p}=\frac{48{{a}^{2}}}{16a}=3a \).
Xét \( \Delta SIK \) có \( SI=IK=r=3a \).
Thể tích khối nón là: \( V=\frac{1}{3}h.\pi {{r}^{2}}=\frac{1}{3}.3a.\pi .{{(3a)}^{2}}=9\pi {{a}^{3}} \).
Câu 15. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Tính diện tích xung quanh \( {{S}_{xq}} \) của hình nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn nội tiếp hình vuông ABCD.
A. \( {{S}_{xq}}=\pi {{a}^{2}}\sqrt{17} \).
B. \( {{S}_{xq}}=\frac{\pi {{a}^{2}}\sqrt{17}}{2} \).
C. \( {{S}_{xq}}=\frac{\pi {{a}^{2}}\sqrt{17}}{4} \).
D. \( {{S}_{xq}}=2\pi {{a}^{2}}\sqrt{17} \).
Hướng dẫn giải:
Chọn C
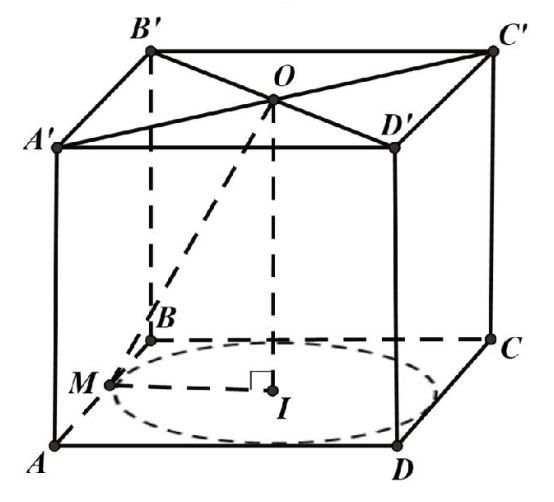
Bán kính đáy của hình nón: \( R=\frac{a}{2} \).
Đường sinh của hình nón: \( \ell =OM\Leftrightarrow \ell =\sqrt{M{{I}^{2}}+O{{I}^{2}}}\Leftrightarrow \ell =\sqrt{{{\left( \frac{a}{2} \right)}^{2}}+4{{a}^{2}}}=\frac{a\sqrt{17}}{2} \).
Đường thẳng xung quanh của hình nón là \( S=\pi .R.\ell =\pi .\frac{a}{2}.\frac{a\sqrt{17}}{2}=\frac{\pi {{a}^{2}}\sqrt{17}}{4} \).
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









