Trung Tâm Luyện Thi Đại Học
Dạng 3. Khối tròn xoay nội, ngoại tiếp khối đa diện - Hình trụ
A. Công thức tính Khối tròn xoay nội, ngoại tiếp khối đa diện - Hình trụ
Trường hợp
B. Bài tập có hướng dẫn giải
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng HSG Toán Lý Hóa các lớp - Ôn thi vào lớp 10 Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
Câu 1. (Đề Tham Khảo – 2018) Cho tứ diện đều ABCD có cạnh bằng 4. Tính diện tích xung quanh \( {{S}_{xq}} \) của hình trụ có một đường tròn đáy là đường tròn nội tiếp tam giác BCD và chiều cao bằng chiều cao của tứ diện ABCD.
A. \({{S}_{xq}}=8\sqrt{3}\pi \).
B. \({{S}_{xq}}=8\sqrt{2}\pi \).
C. \({{S}_{xq}}=\frac{16\sqrt{3}\pi }{3}\).
D. \({{S}_{xq}}=\frac{16\sqrt{2}\pi }{3}\).
Hướng dẫn giải:
Chọn D
Bán kính đường tròn đáy hình trụ bằng một phần ba đường cao tam giác BCD nên \( r=\frac{1}{3}.\frac{4\sqrt{3}}{2}=\frac{2\sqrt{3}}{3} \).
Chiều cao hình trụ bằng chiều cao hình chóp là: \( h=\sqrt{{{4}^{2}}-{{\left( \frac{2}{3}.\frac{4\sqrt{3}}{2} \right)}^{2}}}=\sqrt{16-\frac{16.3}{9}}=\frac{4\sqrt{2}}{\sqrt{3}} \).
Vậy \( {{S}_{xq}}=2\pi rh=2\pi .\frac{2\sqrt{3}}{3}.\frac{4\sqrt{2}}{\sqrt{3}}=\frac{16\sqrt{2}\pi }{3} \).
Câu 2. (Đề Tham Khảo – 2017) Tính thể tích V của khối trụ ngoại tiếp hình lập phương có cạnh bằng a.
A. \( V=\frac{\pi {{a}^{3}}}{6} \).
B. \( V=\frac{\pi {{a}^{3}}}{2} \).
C. \( V=\frac{\pi {{a}^{3}}}{4} \).
D. \( V=\pi {{a}^{3}} \).
Hướng dẫn giải:
Chọn B
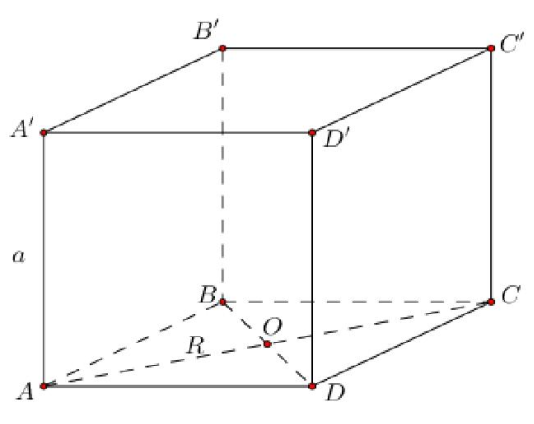
Bán kính đường tròn đáy là \( R=\frac{AC}{2}=\frac{a\sqrt{2}}{2} \); chiều cao \( h=a \).
Vậy thể tích khối trụ là: \( V=\pi {{R}^{2}}h=\pi .\frac{{{a}^{2}}}{2}.a=\frac{\pi {{a}^{3}}}{2} \).
Câu 3. Cho hình lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng a và chiều cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho.
A. \( V=3\pi {{a}^{2}}h \).
B. \( V=\pi {{a}^{2}}h \).
C. \( V=\frac{\pi {{a}^{2}}h}{9} \).
D. \( V=\frac{\pi {{a}^{2}}h}{3} \).
Hướng dẫn giải:
Chọn D
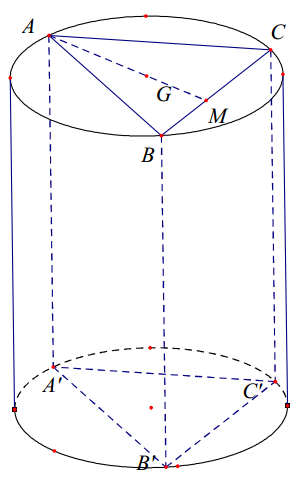
Gọi G là trọng tâm của tam giác ABC. Do ABC là tam giác đều nên G là tâm đường tròn ngoại tiếp tam giác ABC.
Ta có \( AG=\frac{2}{3}AM=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3} \).
Vậy thể tích của khối trụ cần tìm là \( V=\pi {{R}^{2}}h=\pi .{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}h=\frac{\pi {{a}^{2}}h}{3} \) (đvtt).
Câu 4. Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh bằng \( 36\pi {{a}^{2}} \). Tính thể tích V của lăng trụ lục giác đều nội tiếp hình trụ.
A. \( 27\sqrt{3}{{a}^{3}} \).
B. \( 24\sqrt{3}{{a}^{3}} \).
C. \( 36\sqrt{3}{{a}^{3}} \).
D. \( 81\sqrt{3}{{a}^{3}} \).
Hướng dẫn giải:
Chọn D
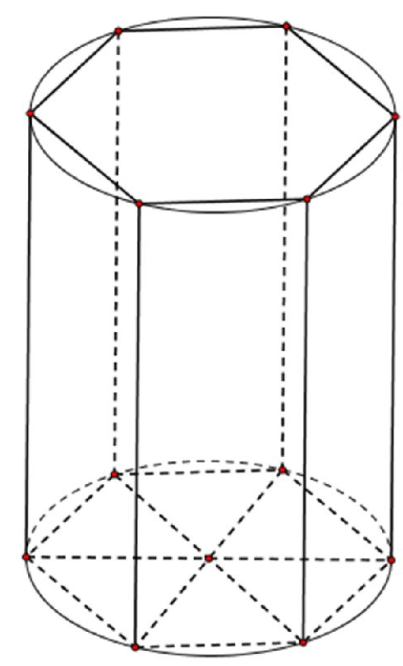
Ta có: \( {{S}_{xq}}=36\pi {{a}^{2}}=2\pi Rh \).
Do thiết diện qua trục là hình vuông nên ta có \( 2R=h \).
Khi đó \( {{h}^{2}}=36{{a}^{2}} \) hay \( h=6a;\,\,R=3a \).
Diện tích của mặt đáy hình lăng trụ lục giác đều nội tiếp hình trụ là \( B=6.\frac{{{R}^{2}}\sqrt{3}}{4}=\frac{27{{a}^{2}}\sqrt{3}}{2} \).
Thể tích V của lăng trụ lục giác đều nội tiếp hình trụ là \( V=B.h=81{{a}^{3}}\sqrt{3} \).
Câu 5. Cho hình trụ (T) chiều cao bằng 2a, hai đường tròn đáy của (T) có tâm lần lượt là O và O1, bán kính bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O1 lấy điểm B sao cho \( AB=a\sqrt{5} \). Thể tích khối tứ diện OO1AB bằng
A. \( \frac{{{a}^{3}}\sqrt{3}}{12} \).
B. \( \frac{{{a}^{3}}\sqrt{3}}{4} \).
C. \( \frac{{{a}^{3}}\sqrt{3}}{6} \).
D. \( \frac{{{a}^{3}}\sqrt{3}}{3} \).
Hướng dẫn giải:
Chọn C
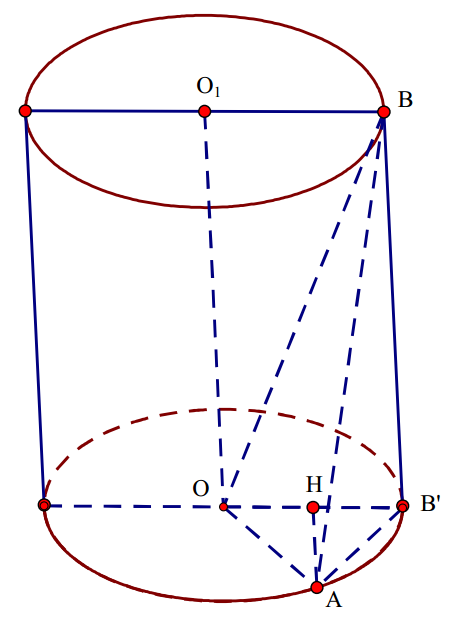
Kẻ đường sinh BB’ và gọi H là trung điểm OB’.
Trong tam giác vuông ABB’ có \( BB’=O{{O}_{1}}=2a \) và \( AB=a\sqrt{5} \) nên \( AB’=\sqrt{A{{B}^{2}}-B{{{{B}’}}^{2}}}=a \).
Tam giác \( OAB’ \) có \( OB’=OA=AB’=a \) nên \( OAB’ \) là tam giác đều \( \Rightarrow AH\bot OB’,\,\,AH=\frac{a\sqrt{3}}{2} \).
Ta có \( \left\{ \begin{align} & AH\bot OB’ \\ & AH\bot O{{O}_{1}} \\ \end{align} \right.\Rightarrow AH\bot ({{O}_{1}}OB) \)
\( \Rightarrow \) Thể tích khối tứ diện \( A.{{O}_{1}}OB \) là
\( {{V}_{{{O}_{1}}OAB}}=\frac{1}{3}AH.{{S}_{\Delta {{O}_{1}}OB}}=\frac{1}{6}AH.{{O}_{1}}O.{{O}_{1}}B=\frac{1}{6}.\frac{a\sqrt{3}}{2}.2a.a=\frac{{{a}^{3}}\sqrt{3}}{6} \).
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng HSG Toán Lý Hóa các lớp - Ôn thi vào lớp 10 Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
Câu 6. Cho khối trụ có đáy là các đường tròn tâm \( (O),\,\,(O’) \) có bán kính là R và chiều cao \( h=R\sqrt{2} \). Gọi A, B lần lượt là các điểm thuộc (O) và (O’) sao cho OA vuông góc với O’B. Tỉ số thể tích của khối tứ diện \( OO’AB \) với thể tích khối trụ là:
A. \( \frac{2}{3\pi } \).
B. \( \frac{1}{3\pi } \).
C. \( \frac{1}{6\pi } \).
D. \( \frac{1}{4\pi } \).
Hướng dẫn giải:
Chọn C
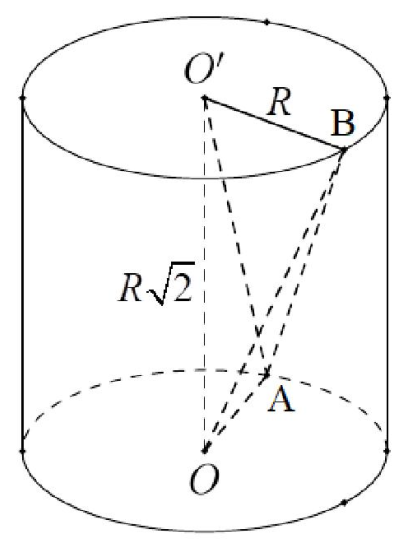
Thể tích khối trụ \( {{V}_{1}}=\pi {{R}^{2}}.h=\pi {{R}^{2}}.R\sqrt{2}=\pi {{R}^{3}}\sqrt{2} \).
Khối tứ diện \( BO’OA \) có \( BO’ \) là đường cao và đáy là tam giác vuông \( O’OA \), do đó thể tích khối tứ diện là
\( {{V}_{2}}=\frac{1}{3}{{S}_{\Delta O’OA}}.O’B=\frac{1}{3}.\frac{1}{2}.OA.OO’.O’B=\frac{1}{6}R.R\sqrt{2}.R=\frac{{{R}^{3}}\sqrt{2}}{6} \).
Vậy \( \frac{{{V}_{2}}}{{{V}_{1}}}=\frac{{{R}^{3}}\sqrt{2}}{6}.\frac{1}{\pi {{R}^{3}}\sqrt{2}}=\frac{1}{6\pi } \).
Câu 7. Một hình trụ có bán kính đáy bằng chiều cao và bằng a. Một hình vuông ABCD có đáy AB, CD là hai dây cung của hai đường tròn đáy và (ABCD) không vuông góc với đáy. Diện tích hình vuông đó bằng
A. \( \frac{5{{a}^{2}}}{4} \).
B. \( 5{{a}^{2}} \).
C. \( \frac{5{{a}^{2}}\sqrt{2}}{2} \).
D. \( \frac{5{{a}^{2}}}{2} \).
Hướng dẫn giải:
Chọn D
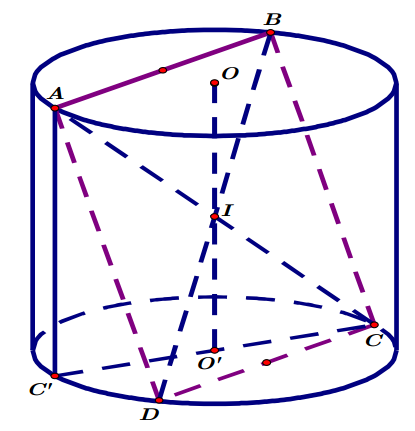
+ Gọi \( O,\,\,O’ \) là tâm của 2 đường tròn đáy, I là trung điểm của \( OO’ \).
Do tính đối xứng nên I là trung điểm của AC, BD.
Kẻ đường kính \( CC’\Rightarrow AC’=a;\,\,CC’=2a\Rightarrow AC=\sqrt{C'{{A}^{2}}+C'{{C}^{2}}}=a\sqrt{5} \).
+ Do đó \( {{S}_{ABCD}}=\frac{1}{2}A{{C}^{2}}=\frac{5{{a}^{2}}}{2} \).
Câu 8. Cho hình lăng trụ đều ABC.A’B’C’, biết góc giữa hai mặt phẳng \( (A’BC) \) và \( (ABC) \) bằng \( 45{}^\circ \) , diện tích tam giác \( A’BC \) bằng \( {{a}^{2}}\sqrt{6} \). Tính diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’.
A. \( \frac{4\pi {{a}^{2}}\sqrt{3}}{3} \).
B. \( 2\pi {{a}^{2}} \).
C. \( 4\pi {{a}^{2}} \).
D. \( \frac{8\pi {{a}^{2}}\sqrt{3}}{3} \).
Hướng dẫn giải:
Chọn C
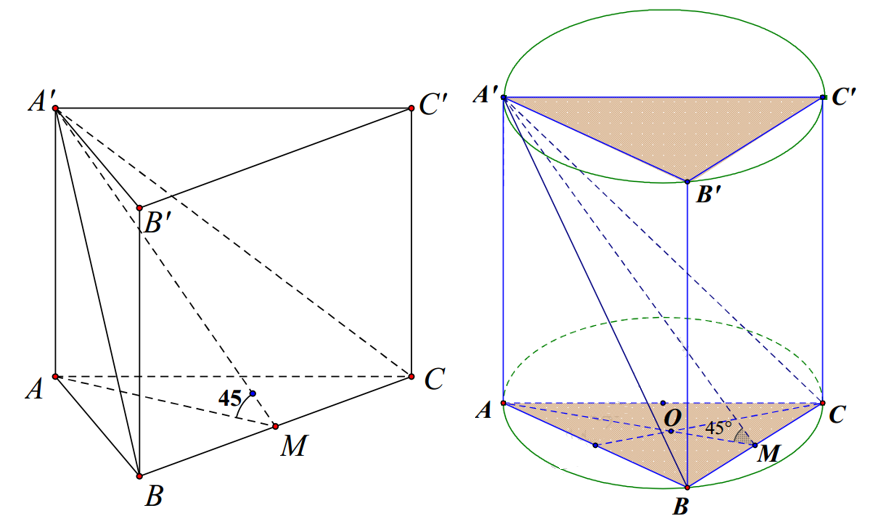
Gọi M là trung điểm BC, khi đó \( \left\{ \begin{align} & BC\bot AM \\ & BC\bot AA’ \\ \end{align} \right.\Rightarrow BC\bot A’M \), do đó \( \left( (A’BC),(ABC) \right)=\widehat{A’MA}=45{}^\circ \) .
Tam giác \( A’AM \) vuông cân tại A nên \( A’M=AM\sqrt{2}=\frac{BC\sqrt{3}}{2}.\sqrt{2}=\frac{BC\sqrt{6}}{2} \).
Diện tích \( {{S}_{A’BC}}=\frac{1}{2}A’M.BC=\frac{1}{2}\frac{BC\sqrt{6}}{2}.BC=\frac{B{{C}^{2}}\sqrt{6}}{4} \).
Theo đề \( \frac{B{{C}^{2}}\sqrt{6}}{4}={{a}^{2}}\sqrt{6}\Rightarrow BC=2a \).
Hình trụ có đáy là đường tròn ngoại tiếp ABC có bán kính \( r=\frac{BC\sqrt{3}}{3}=\frac{2a\sqrt{3}}{3} \), đường cao \( h=AA’=AM=\frac{BC\sqrt{3}}{2}=a\sqrt{3} \).
Diện tích xung quanh \( S=2\pi rh=2\pi .\frac{2a\sqrt{3}}{3}.a\sqrt{3}=4\pi {{a}^{2}} \).
Câu 9. Cho hình trụ có bán kính R và chiều cao \( \sqrt{3}R \). Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục d của hình trụ bằng \( 30{}^\circ \) . Tính khoảng cách giữa AB và trục của hình trụ:
A. \( d\left( AB,d \right)=\frac{R\sqrt{3}}{2} \).
B. \( d\left( AB,d \right)=R \).
C. \( d\left( AB,d \right)=R\sqrt{3} \).
D. \( d\left( AB,d \right)=\frac{R}{2} \).
Hướng dẫn giải:
Chọn A
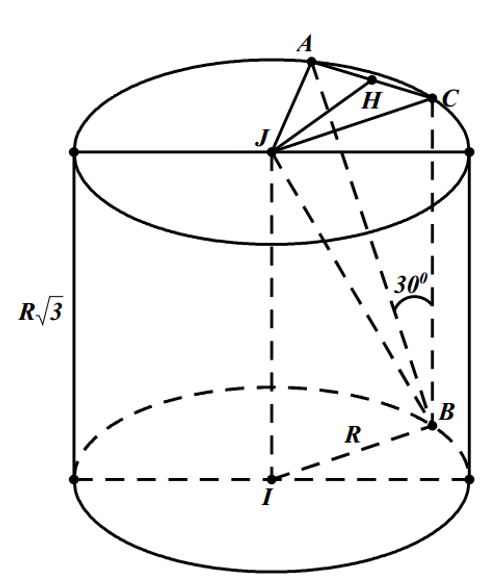
Gọi I,J là tâm của hai đáy (hình vẽ).
Từ B kẻ đường thẳng song song với trục d của hình trụ, cắt đường tròn đáy kia tại C.
Khi đó, \( \left( AB,d \right)=\left( AB,BC \right)=\widehat{ABC}=30{}^\circ \).
Xét tam giác ABC vuông tại C, ta có:
\( \tan \widehat{ABC}=\frac{AC}{CB}\Rightarrow AC=CB.\tan \widehat{ABC}=R\sqrt{3}.\tan 30{}^\circ =R\sqrt{3}.\frac{1}{\sqrt{3}}=R \).
Lại có \(d\parallel (ABC)\) và \(AB\subset (ABC)\) nên \( d\left( d,AB \right)=d\left( d,(ABC) \right)=d\left( J,(ABC) \right) \).
Kẻ \( JH\bot AC,\,\,H\in AC \). Vì \( BC\bot JH \) nên \( JH\bot (ABC) \).
Suy ra \( d\left( J,(ABC) \right)=JH \).
Xét tam giác JAC, ta thấy \( JA=JC=AC=R \) nên JAC là tam giác đều cạnh R.
Khi đó chiều cao là \( JH=\frac{R\sqrt{3}}{2} \).
Vậy \( d\left( d,AB \right)=\frac{R\sqrt{3}}{2} \).
Câu 10. Cho lăng trụ đứng ABC.A’B’C’ có độ dài cạnh bên bằng 2a, đáy ABC là tam giác vuông cân tại A, góc giữa \( AC’ \) và mặt phẳng \( (BCC’B’) \) bằng \( 30{}^\circ \) (tham khảo hình vẽ). Thể tích của khối trụ ngoại tiếp lăng trụ ABC.A’B’C’ bằng
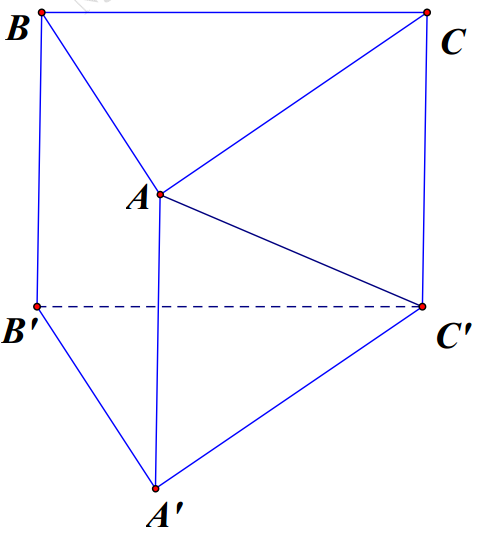
A. \( \pi {{a}^{3}} \).
B. \( 2\pi {{a}^{3}} \).
C. \( 4\pi {{a}^{3}} \).
D. \( 3\pi {{a}^{3}} \).
Hướng dẫn giải:
Chọn C
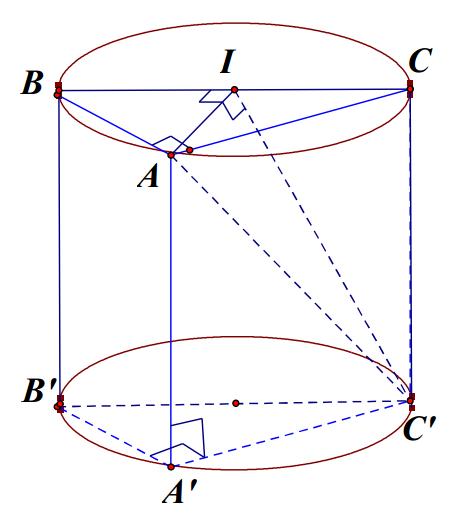
Gọi bán kính của hình trụ là R.
Ta có: \( CC’\bot (ABC)\Rightarrow CC’\bot AI \).
Lại có tam giác ABC là tam giác vuông cân tại A nên \( AI\bot BC \) do đó \( AI\bot (BCC’B’) \) hay góc \( \left( AC’,(BCC’B’) \right)=\widehat{IC’A} \).
Xét tam giác \( AIC’ \) ta có: \( IC’=\frac{AI}{\tan \widehat{IC’A}}=R\sqrt{3} \).
Xét tam giác \( CIC’ \) ta có: \( IC{{‘}^{2}}=I{{C}^{2}}+CC{{‘}^{2}}\Leftrightarrow 3{{R}^{2}}={{R}^{2}}+4{{a}^{2}}\Rightarrow R=a\sqrt{2} \).
Thể tích khối trụ ngoại tiếp lăng trụ ABC.A’B’C’ là: \( V=\pi {{R}^{2}}h=4\pi {{a}^{3}} \).
Câu 11. Cho hình trụ (T) có (C) và (C’) là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhật kích thước \( a\times 2a \) (như hình vẽ dưới đây). Tính thể tích V của khối trụ (T) theo a.
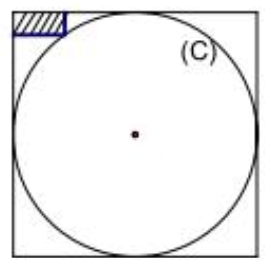
A. \( \frac{100\pi {{a}^{3}}}{3} \).
B. \( 250\pi {{a}^{3}} \).
C. \( \frac{250\pi {{a}^{3}}}{3} \).
D. \( 100\pi {{a}^{3}} \).
Hướng dẫn giải:
Chọn B
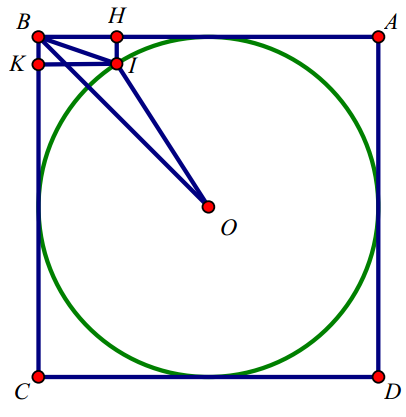
Ta có \( BK=2a,\,\,KI=a \) nên \( BI=a\sqrt{5}\Rightarrow \cos \widehat{KBI}=\frac{1}{\sqrt{5}} \) và \( \sin \widehat{KBI}=\frac{2}{\sqrt{5}} \).
Khi đó \( \cos \widehat{OBI}=\cos \left( \widehat{KBI}-\widehat{KBO} \right)=\cos \widehat{KBI}.\cos 45{}^\circ +\sin \widehat{KBI}.\sin 45{}^\circ \)
\( =\frac{1}{\sqrt{5}}.\frac{\sqrt{2}}{2}+\frac{2}{\sqrt{5}}.\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{2\sqrt{5}} \).
Kí hiệu \( AB=2x \) thì \( OI=x,\,\,OB=x\sqrt{2} \).
Ta có: \( O{{I}^{2}}=B{{O}^{2}}+B{{I}^{2}}-2.BO.BI.\cos \widehat{OBI}=2{{x}^{2}}+5{{a}^{2}}-2.x\sqrt{2}.a\sqrt{5}.\frac{3\sqrt{2}}{2\sqrt{5}}=2{{x}^{2}}+5{{a}^{2}}-6xa \)
\( \Leftrightarrow {{x}^{2}}=2{{x}^{2}}+5{{a}^{2}}-6xa\Leftrightarrow {{x}^{2}}-6xa+5{{a}^{2}}=0\Leftrightarrow \left[ \begin{align} & x=a \\ & x=5a \\ \end{align} \right. \).
Vì \( x>a \) nên \( x=5a \) hay \( r=OI=5a \).
Vậy thể tích khối trụ (T) là \( V=\pi .{{(5a)}^{2}}.10a=250\pi {{a}^{3}} \).
Câu 12. Cho hình trụ có thiết diện qua trục là hình vuông ABCD cạnh bằng \( 2\sqrt{3}\,\,cm \) với AB là đường kính của đường tròn đáy tâm O. Gọi M là điểm thuộc cung \( \overset\frown{AB} \) của đường tròn đáy sao cho \( \widehat{ABM}=60{}^\circ \) . Thể tích của khối tứ diện ACDM là:
A. \( V=3\,\,c{{m}^{3}} \).
B. \( V=4\,\,c{{m}^{3}} \).
C. \( V=6\,\,c{{m}^{3}} \).
D. \( V=7\,\,c{{m}^{3}} \).
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Bồi dưỡng HSG Toán Lý Hóa các lớp - Ôn thi vào lớp 10 Chuyên
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
Hướng dẫn giải:
Chọn A
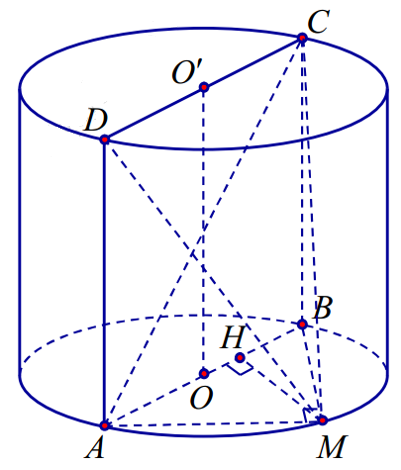
Ta có: \( \Delta MAB \) vuông tại M có \( \widehat{B}=60{}^\circ \) nên \( MB=\sqrt{3},\,\,MA=3 \).
Gọi H là hình chiếu của M lên AB, suy ra \( MH\bot (ACD) \) và \( MH=\frac{MB.MA}{AB}=\frac{3}{2} \).
Vậy \( {{V}_{M.ACD}}=\frac{1}{3}MH.{{S}_{ACD}}=\frac{1}{3}.\frac{3}{2}.6=3\,\,c{{m}^{3}} \).
Câu 13. Cho hình trụ có hai đáy là các hình tròn (O), (O’) bán kính bằng a, chiều cao hình trụ gấp hai lần bán kính đáy. Các điểm A, B tương ứng nằm trên hai đường tròn (O), (O’) sao cho \( AB=a\sqrt{6} \). Tính thể tích khối tứ diện \( ABOO’ \) theo a.
A. \( \frac{{{a}^{3}}}{3} \).
B. \( \frac{{{a}^{3}}\sqrt{5}}{3} \).
C. \( \frac{2{{a}^{3}}}{3} \).
D. \( \frac{2\sqrt{5}{{a}^{3}}}{3} \).
Hướng dẫn giải:
Chọn A
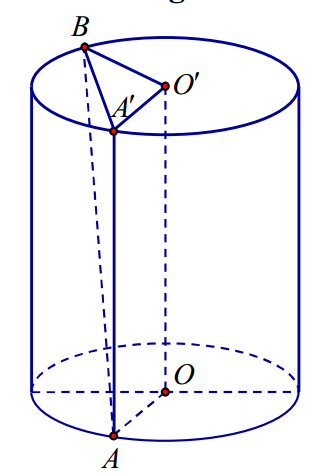
Ta có \( OO’=2a,\,\,A’B=\sqrt{A{{B}^{2}}-AA{{‘}^{2}}}=\sqrt{6{{a}^{2}}-4{{a}^{2}}}=a\sqrt{2} \).
Do đó \( A'{{B}^{2}}=O'{{B}^{2}}+O’A{{‘}^{2}}=2{{a}^{2}} \) nên tam giác \( O’A’B \) vuông cân tại \( O’ \) hay \( O’A’\bot O’B\Rightarrow OA\bot O’B \).
Khi đó \( {{V}_{OO’AB}}=\frac{1}{6}OA.O’B.d\left( OA,O’B \right).\sin \left( OA,O’B \right)=\frac{1}{6}a.a.2a.\sin 90{}^\circ =\frac{{{a}^{3}}}{3} \).
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









