Trung Tâm Luyện Thi Đại Học
Dạng 4. Giải phương trình mũ bằng Phương pháp hàm số, đánh giá
A. Giải phương trình mũ bằng Phương pháp hàm số, đánh giá
Thông thường ta sẽ vừa đủ nội dụng các định lí (và các kết quả) sau:
+ Nếu hàm số y = f(x) đơn điệu một chiều trên D thì phương trình f(x) = 0 không quá một nghiệm trên D.
\( \Rightarrow \)Để vừa đủ định lí này, ta cần nhẩm được 1 nghiệm \( x={{x}_{0}} \) của phương trình, rồi chỉ rõ hàm đơn điệu một chiều trên D (luôn đồng biến hoặc luôn nghịch biến trên D) và kết luận \( x={{x}_{0}} \) là nghiệm duy nhất.
+ Hàm số f(t) đơn điệu một chiều trên khoảng (a;b) và tồn tại u; \( v\in (a;b) \) thì \( f(u)=f(v)\Leftrightarrow u=v \).
\( \Rightarrow \) Để áp dụng định lí này, ta cần xây dựng hàm đặc trưng f(t).
B. Bài tập có hướng dẫn giải
Câu 1. Tổng tất cả các nghiệm thực của phương trình \( 15x{{.5}^{x}}={{5}^{x+1}}+27x+23 \) bằng
A. -1.
B. 2.
C. 1.
D. 0.
Hướng dẫn giải:
Chọn D
Ta có: \( 15x{{.5}^{x}}={{5}^{x+1}}+27x+23\Leftrightarrow {{5}^{x+1}}(3x-1)=27x+23\,\,\,(1) \)
Dễ thấy \( x=\frac{1}{3} \) không thỏa mãn phương trình trên nên ta có:
\( {{5}^{x+1}}(3x-1)=27x+23\Leftrightarrow {{5}^{x+1}}=\frac{27x+23}{3x-1}\,\,\,(2) \)
Hàm số \( y=f(x)={{5}^{x+1}}={{5.5}^{x}} \) đồng biến trên \( \mathbb{R} \).
Hàm số \( y=g(x)=\frac{27x+23}{3x-1} \), có đạo hàm \( {g}'(x)=-\frac{96}{{{(3x-1)}^{2}}}<0 \), nên nghịch biến trên mỗi khoảng \( \left( -\infty ;\frac{1}{3} \right) \) và \( \left( \frac{1}{3};+\infty \right) \).
Do đó trên mỗi khoảng \( \left( -\infty ;\frac{1}{3} \right) \) và \( \left( \frac{1}{3};+\infty \right) \), phương trình (2) có nhiều nhất một nghiệm.
Ta thấy \( x=-1 \) và \( x=1 \) là các nghiệm lần lượt thuộc các khoảng \( \left( -\infty ;\frac{1}{3} \right) \) và \( \left( \frac{1}{3};+\infty \right) \).
Do đó (2) và (1) có hai nghiệm \( x=-1 \) và \( x=1 \).
Tổng hai nghiệm này bằng 0.
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
Câu 2. Cho số thực \( \alpha \) sao cho phương trình \( {{2}^{x}}-{{2}^{-x}}=2\cos (\alpha x) \) có đúng 2019 nghiệm thực. Số nghiệm của phương trình \( {{2}^{x}}+{{2}^{-x}}=4+2\cos (\alpha x) \) là:
A. 2019.
B. 2018.
C. 4037.
D. 4038.
Hướng dẫn giải:
Chọn D
Ta có: \( {{2}^{x}}+{{2}^{-x}}=4+2\cos (\alpha x)\Leftrightarrow {{\left( {{2}^{\frac{x}{2}}}-{{2}^{-\frac{x}{2}}} \right)}^{2}}=2.2{{\cos }^{2}}\left( \alpha .\frac{x}{2} \right) \)
\( \Leftrightarrow \left[ \begin{align} & {{2}^{\frac{x}{2}}}-{{2}^{-\frac{x}{2}}}=2\cos \left( \alpha .\frac{x}{2} \right)\,\,\,\,\,(1) \\ & {{2}^{\frac{x}{2}}}-{{2}^{-\frac{x}{2}}}=-2\cos \left( \alpha .\frac{x}{2} \right)\,\,\,\,\,(2) \\ \end{align} \right. \).
Ta thấy, nếu phương trình \( {{2}^{x}}-{{2}^{-x}}=2\cos (\alpha x) \) có 2019 nghiệm thực thì phương trình (1) cũng có 2019 nghiệm thực.
Nhận xét:
+ \( {{x}_{0}} \) là nghiệm của phương trình (1) \( \Leftrightarrow {{x}_{0}} \) là nghiệm của phương trình (2).
+ \( {{x}_{0}}=0 \) không là nghiệm của hai phương trình (1), (2).
Do đó, tổng số nghiệm của cả hai phương trình (1), (2) là 4038.
Vậy phương trình \( {{2}^{x}}+{{2}^{-x}}=4+2\cos (\alpha x) \) có 4038 nghiệm thực.
Câu 3. Biết \( {{x}_{1}},\,{{x}_{2}} \) là hai nghiệm của phương trình \( {{\log }_{7}}\left( \frac{4{{x}^{2}}-4x+1}{2x} \right)+4{{x}^{2}}+1=6x \) và \( {{x}_{1}}+2{{x}_{2}}=\frac{1}{4}\left( a+\sqrt{b} \right) \) với a, b là hai số nguyên dương. Tính a + b.
A. \( a+b=13 \).
B. \( a+b=11 \).
C. \( a+b=16 \).
D. \( a+b=14 \).
Hướng dẫn giải:
Chọn C
Điều kiện: \( x>0;\,\,x\ne \frac{1}{2} \).
Ta có: \( {{\log }_{7}}\left( \frac{4{{x}^{2}}-4x+1}{2x} \right)+4{{x}^{2}}+1=6x\Leftrightarrow {{\log }_{7}}(4{{x}^{2}}-4x+1)+4{{x}^{2}}-4x+1={{\log }_{7}}(2x)+2x \).
Xét hàm số \( f(t)={{\log }_{7}}t+t\) có \( {f}'(t)=\frac{1}{t\ln 7}+1>0,\,\,\forall t>0 \) nên là hàm số đồng biến trên \( (0;+\infty ) \).
Do đó, ta có \( 4{{x}^{2}}-4x+1=2x\Leftrightarrow 4{{x}^{2}}-6x+1=0\Leftrightarrow x=\frac{3\pm \sqrt{5}}{4} \).
Khi đó: \( {{x}_{1}}+2{{x}_{2}}=\frac{3-\sqrt{5}}{4}+2.\frac{3+\sqrt{5}}{4}=\frac{1}{4}\left( 9+\sqrt{5} \right)\) hoặc \( {{x}_{1}}+2{{x}_{2}}=\frac{3+\sqrt{5}}{4}+2.\frac{3-\sqrt{5}}{4}=\frac{1}{4}\left( 9-\sqrt{5} \right) \) .
Vậy \( {{x}_{1}}=\frac{3-\sqrt{5}}{4};\,\,{{x}_{2}}=\frac{3+\sqrt{5}}{4} \).
Do đó: \( a=9;\,\,b=5 \) và \( a+b=9+5=14 \).
Câu 4. Phương trình \( x\left( {{2}^{x-1}}+4 \right)={{2}^{x+1}}+{{x}^{2}} \) có tổng các nghiệm bằng
A. 7.
B. 3.
C. 5.
D. 6.
Hướng dẫn giải:
Chọn A
Ta có: \( x\left( {{2}^{x-1}}+4 \right)={{2}^{x+1}}+{{x}^{2}}\Leftrightarrow x{{.2}^{x-1}}-{{4.2}^{x-1}}+4x-{{x}^{2}}=0 \)
\( \Leftrightarrow {{2}^{x-1}}(x-4)-x(x-4)=0\Leftrightarrow (x-4)({{2}^{x-1}}-x)=0\Leftrightarrow \left[ \begin{align} & x=4 \\ & {{2}^{x}}=2x\,\,\,\,\,\,(*) \\ \end{align} \right. \).
Giải phương trình (*):
Xét hàm số \( f(x)={{2}^{x}}-2x có {f}'(x)={{2}^{x}}\ln 2-2;\,\,{f}”(x)={{2}^{x}}{{\ln }^{2}}2>0 \).
Suy ra phương trình \( {f}'(x)=0 \) có duy nhất một nghiệm, suy ra phương trình \( f(x)=0 \) có nhiều nhất là hai nghiệm. Mà ta thấy \( f(1)=f(2)=0 \) nên phương trình (*) có 2 nghiệm \( x=1;\,\,x=2 \).
Vậy tổng các nghiệm của phương trình là 7.
Câu 5. Tìm số nghiệm của phương trình \( {{\left( \left| x \right|-1 \right)}^{2}}{{e}^{\left| x \right|-1}}-\log 2=0 \).
A. 4.
B. 3.
C. 2.
D. 0.
Hướng dẫn giải:
Chọn A
Tập xác định: \( D=\mathbb{R} \).
Đặt \( t=\left| x \right|-1\ge -1 \), với \( t\ge -1\Rightarrow \left| x \right|=t+1\Leftrightarrow \left[ \begin{align} & x=t+1 \\ & x=-t-1 \\ \end{align} \right. \).
Khi đó phương trình trở thành \( {{t}^{2}}{{e}^{t}}-\log 2=0\,\,\,\,\,\,\,\,(1) \)
Số nghiệm của phương trình (1) là số điểm chung của đồ thị hàm số \( y=f(t)={{t}^{2}}{{e}^{t}}-\log 2 \) và đường thẳng \( y=0 \).
Ta có: \( {f}'(t)={{e}^{t}}({{t}^{2}}+2t)\Rightarrow {f}'(t)=0\Leftrightarrow \left[ \begin{align} & t=0\,\,(n) \\ & t=-2\,\,(\ell ) \\ \end{align} \right. \).
Bảng biến thiên:
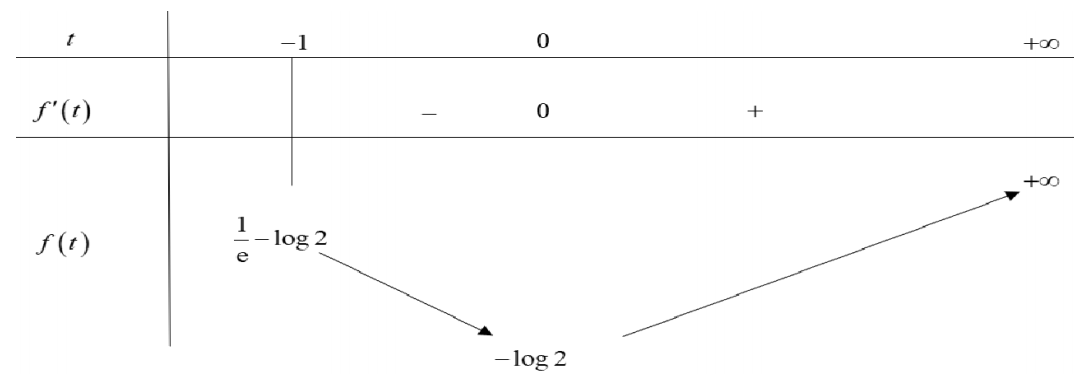
Ta có: \( -\log 2<0<\frac{1}{e}-\log 2 \), dựa vào bảng biến thiên ta được phương trình (1) có 2 nghiệm phân biệt \( {{t}_{1}},{{t}_{2}} \) thỏa mãn \( -1<{{t}_{1}}<{{t}_{2}} \) hay phương trình đã cho có 4 nghiệm x phân biệt.
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
Câu 6. Tính số nghiệm của phương trình \( \cot x={{2}^{x}} \) trong khoảng \( \left( \frac{11\pi }{12};2019\pi \right) \).
A. 2019.
B. 2018.
C. 1.
D. 2020.
Hướng dẫn giải:
Chọn B
Xét phương trình \( \cot x={{2}^{x}}\,\,\,\,\,\,\,\,(1) \).
Điều kiện: \( \sin x\ne 0\Leftrightarrow x\ne k\pi ,\,\,k\in \mathbb{Z} \).
Xét hàm số \( f(x)={{2}^{x}}-\cot x,\,\,x\in \left( \frac{11\pi }{12};2019\pi \right)\backslash \{k\pi \} với k\in \mathbb{Z} \).
\( \Rightarrow {f}'(x)={{2}^{x}}.\ln 2+1+{{\cot }^{2}}x>0,\,\,\forall x\in \left( \frac{11\pi }{12};2019\pi \right)\backslash \{k\pi \} \) với \( k\in \mathbb{Z} \).
Suy ra hàm số f(x) liên tục và đồng biến trên mỗi khoảng \( \left( \frac{11\pi }{12};\pi \right);\,\,(\pi ;2\pi );…;(2018\pi ;2019\pi ) \).
+ Trên khoảng \( \left( \frac{11\pi }{12};\pi \right) \) ta có bảng biến thiên:
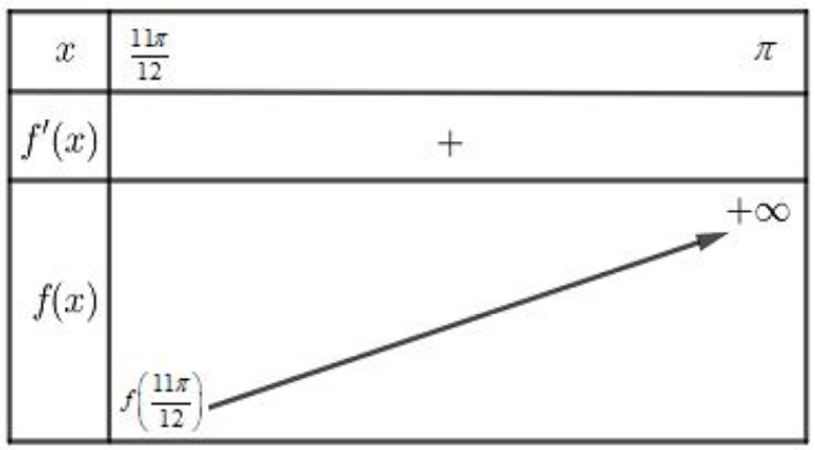
Ta có: \( f\left( \frac{11\pi }{12} \right)={{2}^{\frac{11\pi }{12}}}-\cot \left( \frac{11\pi }{12} \right)\approx 11,0925>0 \). Do đó phương trình \( f(x)=0 \) vô nghiệm trên khoảng \( \left( \frac{11\pi }{12};\pi \right) \).
+ Trên mỗi khoảng \( \left( k\pi ;(k+1)\pi \right),\,\,k\in \{1;2;…;2018\} \) ta có bảng biến thiên:
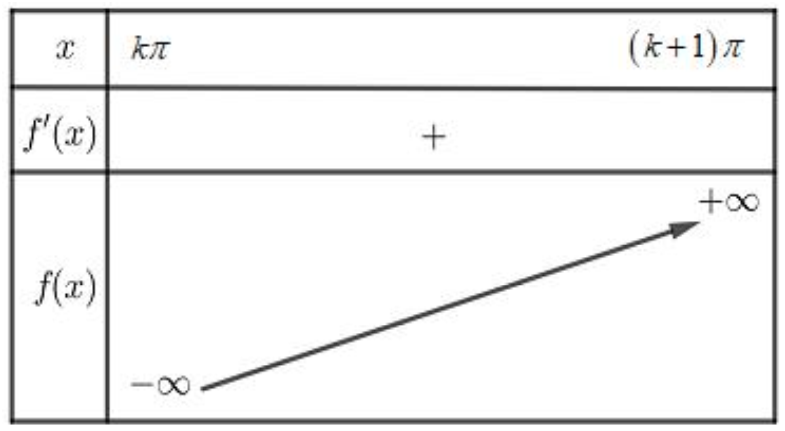
Dựa vào đồ thị hàm số ta thấy mỗi khoảng \( \left( k\pi ;(k+1)\pi \right),\,\,k\in \{1;2;…;2018\} \) phương trình \( f(x)=0 \) có đúng 1 nghiệm. Mà có 2018 khoảng nên phương trình \( f(x)=0 \) có đúng 2018 nghiệm.
Vậy phương trình \( f(x)=0 \) có 2018 nghiệm.
Câu 7. Hỏi phương trình \( {{3.2}^{x}}+{{4.3}^{x}}+{{5.4}^{x}}={{6.5}^{x}} \) có tất cả bao nhiêu nghiệm thực?
A. 0.
B. 1.
C. 3.
D. 2.
Hướng dẫn giải:
Chọn B
Ta có: \( {{3.2}^{x}}+{{4.3}^{x}}+{{5.4}^{x}}={{6.5}^{x}}\Leftrightarrow 3{{\left( \frac{2}{5} \right)}^{x}}+4{{\left( \frac{3}{5} \right)}^{x}}+5{{\left( \frac{4}{5} \right)}^{x}}-6=0 \).
Xét hàm số \( f(x)=3{{\left( \frac{2}{5} \right)}^{x}}+4{{\left( \frac{3}{5} \right)}^{x}}+5{{\left( \frac{4}{5} \right)}^{x}}-6,\,\,\forall x\in \mathbb{R} \).
Có \( {f}'(x)=3{{\left( \frac{2}{5} \right)}^{x}}\ln \frac{2}{5}+4{{\left( \frac{3}{5} \right)}^{x}}\ln \frac{3}{5}+5{{\left( \frac{4}{5} \right)}^{x}}\ln \frac{4}{5}<0,\,\,\forall x\in \mathbb{R} \) nên hàm số f(x) nghịch biến trên \( \mathbb{R} \) suy ra phương trình f(x) = 0 có nhiều nhất một nghiệm (1).
Mặt khác: \( f(1).f(2)=\frac{8}{5}.\left( -\frac{22}{25} \right)=-\frac{176}{125}<0 \) nên phương trình có ít nhất một nghiệm thuộc khoảng (1;2) (2)
Từ (1) và (2) suy ra phương trình đã cho có nghiệm duy nhất.
Câu 8. Phương trình \( {{2019}^{\sin x}}=\sin x+\sqrt{2-{{\cos }^{2}}x} \) có bao nhiêu nghiệm thực trên \( \left[ -5\pi ;2019\pi \right] \)?
A. 2025.
B. 2017.
C. 2022.
D. Vô nghiệm.
Hướng dẫn giải:
Chọn A
Xét \( {{2019}^{\sin x}}=\sin x+\sqrt{2-{{\cos }^{2}}x}\Leftrightarrow {{2019}^{\sin x}}=\sin x+\sqrt{1+{{\sin }^{2}}x}\,\,\,\,\,(1) \)
Đặt \( t=\sin x,\,\,t\in [-1;1] \).
Khi đó (1) trở thành \( {{2019}^{t}}=t+\sqrt{1+{{t}^{2}}}\Leftrightarrow {{2019}^{t}}\left( t-\sqrt{1+{{t}^{2}}} \right)=-1\,\,\,\,\,\,\,(2) \).
Xét hàm số: \( f(t)={{2019}^{t}}\left( t-\sqrt{1+{{t}^{2}}} \right),\,\,\forall t\in [-1;1] \)
\( \Rightarrow {f}'(t)=\frac{{{2019}^{t}}\left( t-\sqrt{1+{{t}^{2}}} \right)\left( \sqrt{1+{{t}^{2}}}\ln 2019-1 \right)}{\sqrt{1+{{t}^{2}}}} \).
Cho \( {f}'(t)=0\Leftrightarrow \left[ \begin{align} & t-\sqrt{1+{{t}^{2}}}=0 \\ & \sqrt{1+{{t}^{2}}}\ln 2019-1=0 \\ \end{align} \right. \) vô nghiệm \( \Rightarrow {f}'(t)<0,\,\,\forall t\in [-1;1] \).
\( \Rightarrow (2) \) có nghiệm duy nhất \( t=0\Rightarrow \sin x=0\Leftrightarrow x=k\pi ,\,\,k\in \mathbb{Z} \).
Mà \( x\in [-5\pi ;2019\pi ]\Rightarrow -5\pi \le k\pi \le 2019\pi \Leftrightarrow -5\le k\le 2019\Rightarrow k\in [-5;2019] \).
Kết luận: Có 2025 nghiệm thực trên \( [-5\pi ;2019\pi ] \).
Câu 9. Số nghiệm của phương trình \( {{3}^{{{\log }_{7}}(x+4)}}=x \) là:
A. 1.
B. 0.
C. 2.
D. 3.
Hướng dẫn giải:
Chọn A
Điều kiện của phương trình: \( x>-4 \).
Với \( x>0 \) phương trình đã cho tương dương với phương trình \( {{\log }_{7}}(x+4)={{\log }_{3}}x \).
Đặt \( {{\log }_{7}}(x+4)={{\log }_{3}}x=t \).
Ta có: \( \left\{ \begin{align} & x+4={{7}^{t}} \\ & x={{3}^{t}} \\ \end{align} \right.\Rightarrow {{7}^{t}}={{3}^{t}}+4\Leftrightarrow {{\left( \frac{3}{7} \right)}^{t}}+4{{\left( \frac{1}{7} \right)}^{t}}-1=0\,\,\,\,\,(1) \)
Xét hàm số \( f(t)={{\left( \frac{3}{7} \right)}^{t}}+4{{\left( \frac{1}{7} \right)}^{t}}-1,\,\,\forall t\in \mathbb{R} \).
Ta có: \( {f}'(t)={{\left( \frac{3}{7} \right)}^{t}}\ln \left( \frac{3}{7} \right)+4{{\left( \frac{1}{7} \right)}^{t}}\ln \left( \frac{1}{7} \right)<0,\,\,\forall t\in \mathbb{R} \)
Nên f(t) nghịch biến trên tập \( \mathbb{R} \).
Mà \( f(1)=0 \) nên phương trình có nghiệm duy nhất \( t=1\Leftrightarrow x=3 \).
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
Câu 10. Cho các số thực x, y với \( x\ge 0 \) thỏa mãn \( {{e}^{x+3y}}+{{e}^{xy+1}}+x(y+1)+1={{e}^{-xy-1}}+\frac{1}{{{e}^{x+3y}}}-3y \). Gọi m là giá trị nhỏ nhất của biểu thức \( T=x+2y+1 \). Mệnh đề nào sau đây là đúng?
A. \( m\in (2;3) \).
B. \( m\in (-1;0) \).
C. \( m\in (0;1) \).
D. \( m\in (1;2) \).
Hướng dẫn giải:
Chọn C
Từ giả thiết \( {{e}^{x+3y}}+{{e}^{xy+1}}+x(y+1)+1={{e}^{-xy-1}}+\frac{1}{{{e}^{x+3y}}}-3y \)
\( \Leftrightarrow {{e}^{x+3y}}-\frac{1}{{{e}^{x+3y}}}+(x+3y)={{e}^{-xy-1}}-\frac{1}{{{e}^{-xy-1}}}+(-xy-1)\,\,\,\,\,\,\,\,\,(1) \)
Xét hàm số \( f(t)={{e}^{t}}-\frac{1}{{{e}^{t}}}+t \) với \( t\in \mathbb{R} \) ta có \( {f}'(t)={{e}^{t}}+\frac{1}{{{e}^{t}}}+1>0,\,\,\forall t\in \mathbb{R}\Rightarrow f(t) \) là hàm số đồng biến trên \( \mathbb{R} \).
Phương trình (1) có dạng \( f(x+3y)=f(-xy-1)\Rightarrow x+3y=-xy-1\Rightarrow y=\frac{-x-1}{x+3}\,\,(x\ge 0) \).
Khi đó \( T=x+2y+1=x-\frac{2x+2}{x+3}+1\Rightarrow T’=1-\frac{4}{{{(x+3)}^{2}}}=\frac{{{x}^{2}}+6x+5}{{{(x+3)}^{2}}}>0,\,\,\forall x\ge 0 \).
\( \Rightarrow {{T}_{\min }}=0-\frac{2.0+2}{0+3}+1=\frac{1}{3}=m \).
Câu 11. Số nghiệm của phương trình \( {{x}^{2}}-5x-2=({{x}^{2}}-8x+3){{.8}^{3x-5}}+(3x-5){{.8}^{{{x}^{2}}-8x+3}} \) là:
A. 4.
B. 3.
C. 1.
D. 2.
Hướng dẫn giải:
Chọn B
Đặt \( \left\{ \begin{align} & u={{x}^{2}}-8x+3 \\ & v=3x-5 \\ \end{align} \right. \), phương trình đã cho trở thành:
\( u+v=u{{.8}^{v}}+v{{.8}^{u}}\Leftrightarrow u(1-{{8}^{v}})=v({{8}^{u}}-1)\,\,\,\,\,\,(*) \)
+Ta thấy \( u=0\vee v=0 \) thỏa mãn phương trình (*).
+ Với \( \left\{ \begin{align} & u\ne 0 \\ & v\ne 0 \\ \end{align} \right. \) ta có \( (*)\Leftrightarrow \frac{1-{{8}^{v}}}{v}=\frac{{{8}^{u}}-1}{u}\,\,\,\,\,(**) \)
Ta thấy:
– Nếu \( u>0 \) thì \( \frac{{{8}^{u}}-1}{u}>0 \) và nếu \( u<0 \) thì \( \frac{{{8}^{u}}-1}{u}>0 \). Do đó \( VP(**)>0,\,\,\forall u\ne 0 \).
– Nếu \( v>0 \) thì \(\frac{1-{{8}^{v}}}{v}<0\) và nếu \(v<0\) thì \(\frac{1-{{8}^{v}}}{v}<0\). Do đó \(VT(**)<0,\,\,\forall v\ne 0\).
Từ đó suy ra (**) vô nghiệm.
Như vậy, phương trình đã cho tương đương với:
\( \left[ \begin{align} & u=0 \\ & v=0 \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & {{x}^{2}}-8x+3=0 \\ & 3x-5=0 \\ \end{align} \right. \) \( \Leftrightarrow \left[ \begin{align} & x=4+\sqrt{13} \\ & x=4-\sqrt{13} \\ & x=\frac{5}{3} \\ \end{align} \right. \).
Vậy, phương trình đã cho có 3 nghiệm.
Câu 12. Tích tất cả các giá trị của x thỏa mãn phương trình \( {{({{3}^{x}}-3)}^{2}}-({{4}^{x}}-4)={{({{3}^{x}}+{{4}^{x}}-7)}^{2}} \) bằng
A. 2.
B. 1.
C. 4.
D. 3.
Hướng dẫn giải:
Chọn B
Phương trình \( \Leftrightarrow ({{3}^{x}}+{{4}^{x}}-7)({{3}^{x}}-{{4}^{x}}+1)={{({{3}^{x}}+{{4}^{x}}-7)}^{2}} \)
\( \Leftrightarrow ({{3}^{x}}+{{4}^{x}}-7)({{2.4}^{x}}-8)=0\Leftrightarrow \left[ \begin{align} & {{2.4}^{x}}=8\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \\ & {{3}^{x}}+{{4}^{x}}-7=0\,\,\,\,\,(2) \\ \end{align} \right. \)
Xét phương trình (1): \( (1)\Leftrightarrow {{4}^{x}}=4\Leftrightarrow x=1 \).
Xét phương trình (2): Xét hàm số \( f(x)={{3}^{x}}+{{4}^{x}}-7 \) trên \( \mathbb{R} \).
Hàm số f(x) liên tục và \( {f}'(x)={{3}^{x}}.\ln 3+{{4}^{x}}.\ln 4>0,\,\,\forall x\in \mathbb{R} \) nên f(x) là hàm số đồng biến trên \( \mathbb{R} \).
Khi đó, \( (2)\Leftrightarrow f(x)=f(1)\Leftrightarrow x=1 \).
Vậy tích các nghiệm của phương trình bằng 1.
Câu 13. Phương trình \( {{e}^{x}}-{{e}^{\sqrt{2x+1}}}=1-{{x}^{2}}+2\sqrt{2x+1} \) có nghiệm trong khoảng nào?
A. \( \left( 2;\frac{5}{2} \right) \).
B. \( \left( \frac{3}{2};2 \right) \).
C. \( \left( 1;\frac{3}{2} \right) \).
D. \( \left( \frac{1}{2};1 \right) \).
Hướng dẫn giải:
Chọn A
Điều kiện: \( x\ge -\frac{1}{2} \).
\( {{e}^{x}}-{{e}^{\sqrt{2x+1}}}=1-{{x}^{2}}+2\sqrt{2x+1}\Leftrightarrow {{e}^{x}}-{{e}^{\sqrt{2x+1}}}=-{{(x+1)}^{2}}+{{\left( \sqrt{2x+1}+1 \right)}^{2}} \)
\( \Leftrightarrow {{e}^{x}}+{{(x+1)}^{2}}={{e}^{\sqrt{2x+1}}}+{{\left( \sqrt{2x+1}+1 \right)}^{2}}\,\,\,\,\,\,\,\,(*) \)
Xét hàm số \( f(t)={{e}^{t}}+{{(t+1)}^{2}} \) với \( t\ge -\frac{1}{2} \).
\( {f}'(t)={{e}^{t}}+2(t+1)>0 \) với mọi \( t\ge -\frac{1}{2} \).
Suy ra hàm số đồng biến trên \( \left[ -\frac{1}{2};+\infty \right) \).
\( (*)\Leftrightarrow f(x)=f\left( \sqrt{2x+1} \right)\Leftrightarrow x=\sqrt{2x+1}\Leftrightarrow \left\{ \begin{align} & x\ge 0 \\ & {{x}^{2}}=2x+1 \\ \end{align} \right. \)
\( \Leftrightarrow \left\{ \begin{align} & x\ge 0 \\ & {{x}^{2}}-2x-1=0 \\ \end{align} \right. \) \( \begin{cases} x\ge 0 \\\left[\begin{array}{l} x=1-\sqrt{2} \\ x=1+\sqrt{2}\end{array}\right.\end{cases} \Leftrightarrow x=1+\sqrt{2}\).
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học từ 1,5h ➜ 2h/1 buổi!
- Học phí giá rẻ - bình dân!
- Đóng 3 tháng tặng 1 tháng
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









