Trung Tâm Luyện Thi Đại Học
Dạng 3. Giải phương trình mũ bằng Phương pháp logarit hóa
A. Giải phương trình mũ bằng Phương pháp logarit hóa
+ Loại 1: Phương trình \( {{a}^{f(x)}}=b\Leftrightarrow \left\{ \begin{align} & 0<a\ne 1,\,\,b>0 \\ & f(x)={{\log }_{a}}b \\ \end{align} \right. \).
+ Loại 2: Phương trình: \( {{a}^{f(x)}}={{b}^{g(x)}}\Leftrightarrow {{\log }_{a}}{{a}^{f(x)}}={{\log }_{a}}{{b}^{f(x)}}\Leftrightarrow f(x)=g(x).{{\log }_{a}}b \)
Hoặc \( {{\log }_{b}}{{a}^{f(x)}}={{\log }_{b}}{{b}^{g(x)}}\Leftrightarrow f(x).{{\log }_{b}}a=g(x) \).
B. Bài tập có hướng dẫn giải
Câu 1. Số giao điểm của các đồ thị hàm số \( y={{3}^{{{x}^{2}}+1}} \) và \( y=5 \) là:
A. 0.
B. 3.
C. 2.
D. 1.
Hướng dẫn giải:
Chọn C
Số giao điểm của hai đồ thị hàm số \( y={{3}^{{{x}^{2}}+1}} \) và \( y=5 \) bằng số nghiệm của phương trình:
\( {{3}^{{{x}^{2}}+1}}=5\Leftrightarrow {{x}^{2}}+1={{\log }_{3}}5\Leftrightarrow {{x}^{2}}={{\log }_{3}}5-1\Leftrightarrow x=\pm \sqrt{{{\log }_{3}}5-1} \).
Vậy số giao điểm của hai đồ thị hàm số \( y={{3}^{{{x}^{2}}+1}} \) và \( y=5 \) bằng 2.
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
- Thời gian học từ 1,5h - 2h/1 buổi!
- Học phí bình dân!
- Đóng 3 tháng tặng 1 tháng
Câu 2. Tính tích các nghiệm thực của phương trình \( {{2}^{{{x}^{2}}-1}}={{3}^{2x+3}} \).
A. \( -3{{\log }_{2}}3 \).
B. \( -{{\log }_{2}}54 \).
C. – 1.
D. \( 1-{{\log }_{2}}3 \).
Hướng dẫn giải:
Chọn B
Phương trình tương đương: \( {{\log }_{2}}{{2}^{{{x}^{2}}-1}}={{\log }_{2}}{{3}^{2x+3}}\Leftrightarrow {{x}^{2}}-1=(2x+3){{\log }_{2}}3 \)
\( \Leftrightarrow {{x}^{2}}-2x.{{\log }_{2}}3-1-3{{\log }_{2}}3=0 \).
Do \( a.c=1.(-1-3{{\log }_{2}}3)<0 \) nên phương trình luôn có 2 nghiệm thực phân biệt \( {{x}_{1}},{{x}_{2}} \).
Theo định lí Viet ta có: \( {{x}_{1}}.{{x}_{2}}=-1-3{{\log }_{2}}3=-{{\log }_{2}}2-{{\log }_{2}}27=-{{\log }_{2}}54 \).
Câu 3. Cho hai số thực \( a>1,\,\,b>1 \). Gọi \( {{x}_{1}},{{x}_{2}} \) là hai nghiệm của phương trình \( {{a}^{x}}.{{b}^{{{x}^{2}}-1}}=1 \). Trong trường hợp biểu thức \( S={{\left( \frac{{{x}_{1}}.{{x}_{2}}}{{{x}_{1}}+{{x}_{2}}} \right)}^{2}}-4{{x}_{1}}-4{{x}_{2}} \) đạt giá trị nhỏ nhất, mệnh đề nào sau đây là đúng?
A. \( a\ge b \).
B. \( a.b=4 \).
C. \( a.b=2 \).
D. \( a<b \).
Hướng dẫn giải:
Chọn D
Ta có: \( {{a}^{x}}.{{b}^{{{x}^{2}}-1}}=1\Leftrightarrow {{x}^{2}}+x{{\log }_{a}}b-1=0 \). Nhận thấy phương trình luôn có hai nghiệm trái dấu.
Theo định lí Viet, ta có: \( {{x}_{1}}+{{x}_{2}}=-{{\log }_{b}}a;\,\,{{x}_{1}}.{{x}_{2}}=-1 \).
Khi đó: \( S={{\left( \frac{{{x}_{1}}.{{x}_{2}}}{{{x}_{1}}+{{x}_{2}}} \right)}^{2}}-4{{x}_{1}}-4{{x}_{2}}=\log _{a}^{2}b+\frac{4}{{{\log }_{a}}b} \).
Đặt \( {{\log }_{a}}b=t,\,\,t>0 \) (Vì \( a>1,\,\,b>1 \)), khi đó:
\( S={{t}^{2}}+\frac{4}{t};\,\,{S}’=2t-\frac{4}{{{t}^{2}}}=\frac{2{{t}^{3}}-4}{{{t}^{2}}};\,\,{S}’=0\Leftrightarrow t=\sqrt[3]{2} \).
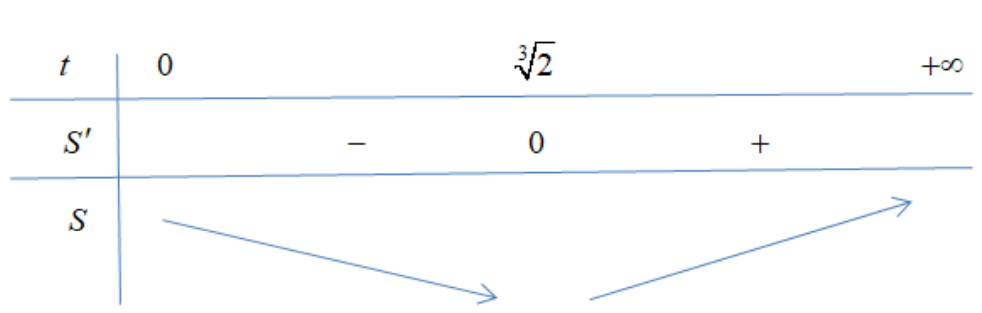
Suy ra biểu thức S đạt giá trị nhỏ nhất tại \( t=\sqrt[3]{2} \) hay \( {{\log }_{a}}b=\sqrt[3]{2}>1\Rightarrow a<b \)
Câu 4. Cho x, y, z là các số thực thỏa mãn \( {{2}^{x}}={{3}^{y}}={{6}^{-z}} \). Giá trị của biểu thức \( M=xy+yz+xz \) là
A. 0.
B. 6.
C. 3.
D. 1.
Hướng dẫn giải:
Chọn A
Đặt \( {{2}^{x}}={{3}^{y}}={{6}^{-z}}=t \) với \( t>0 \).
\( \Rightarrow \left\{ \begin{align} & {{2}^{x}}=t \\ & {{3}^{y}}=t \\ & {{6}^{-z}}=t \\ \end{align} \right. \) \( \Rightarrow \left\{ \begin{align} & x={{\log }_{2}}t \\ & y={{\log }_{3}}t \\ & z=-{{\log }_{6}}t \\ \end{align} \right. \).
Mặt khác: \( {{\log }_{6}}t=\frac{1}{{{\log }_{t}}6}=\frac{1}{{{\log }_{t}}3+{{\log }_{t}}2}=\frac{1}{\frac{1}{{{\log }_{3}}t}+\frac{1}{{{\log }_{2}}t}}=\frac{{{\log }_{3}}t.{{\log }_{2}}t}{{{\log }_{3}}t+{{\log }_{2}}t} \).
\( M=xy+yz+xz={{\log }_{3}}t.{{\log }_{2}}t-{{\log }_{3}}t.{{\log }_{6}}t-{{\log }_{6}}t.{{\log }_{2}}t \)
\( ={{\log }_{3}}t.{{\log }_{2}}t-({{\log }_{3}}t+{{\log }_{2}}t).{{\log }_{6}}t={{\log }_{3}}t.{{\log }_{2}}t-({{\log }_{3}}t+{{\log }_{2}}t).\frac{{{\log }_{3}}t.{{\log }_{2}}t}{{{\log }_{3}}t+{{\log }_{2}}t}=0 \).
Câu 5. Gọi x, y các số thực dương thỏa mãn điều kiện \( {{\log }_{9}}x={{\log }_{6}}y={{\log }_{4}}(x+y) \) và \( \frac{x}{y}=\frac{-a+\sqrt{b}}{2} \), với a, b là hai số nguyên dương. Tính \( T={{a}^{2}}+{{b}^{2}} \).
A. T = 26
T = 29
C. T = 20
D. T = 25
Hướng dẫn giải:
Đáp án A.
Đặt \( t={{\log }_{9}}x={{\log }_{6}}y={{\log }_{4}}(x+y) \), ta có: \( \left\{ \begin{align} & x={{9}^{t}} \\ & y={{6}^{t}} \\ & x+y={{4}^{t}} \\ \end{align} \right.\Rightarrow {{9}^{t}}+{{6}^{t}}={{4}^{t}} \)
\( \Leftrightarrow {{\left( \frac{3}{2} \right)}^{2t}}+{{\left( \frac{3}{2} \right)}^{t}}-1=0\Leftrightarrow \left\{ \begin{align} & {{\left( \frac{3}{2} \right)}^{t}}=\frac{-1-\sqrt{5}}{2}\text{(lo }\!\!{}^\text{1}\!\!\text{ i)} \\ & {{\left( \frac{3}{2} \right)}^{t}}=\frac{-1+\sqrt{5}}{2} \\ \end{align} \right. \)
\( \Rightarrow {{\left( \frac{3}{2} \right)}^{t}}=\frac{-1+\sqrt{5}}{2} \)
Suy ra: \( \frac{x}{y}={{\left( \frac{9}{6} \right)}^{t}}={{\left( \frac{3}{2} \right)}^{t}}=\frac{-1+\sqrt{5}}{2}=\frac{-a+\sqrt{b}}{2} \)
\( \Rightarrow \left\{ \begin{align} & a=1 \\ & b=5 \\ \end{align} \right.\Rightarrow T={{a}^{2}}+{{b}^{2}}={{1}^{2}}+{{5}^{2}}=26 \).
Nhận Dạy Kèm Toán - Lý - Hóa Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Toán - Lý - Hóa từ lớp 6 ➜ 12 - Ôn thi Đại Học - Cao Đẳng
- Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
- Thời gian học từ 1,5h - 2h/1 buổi!
- Học phí bình dân!
- Đóng 3 tháng tặng 1 tháng
Câu 6. Cho các số thực dương a, b thỏa mãn \( {{\log }_{4}}a={{\log }_{6}}b={{\log }_{9}}\left( 4a-5b \right)-1 \). Đặt \( T=\frac{b}{a} \). Khẳng định nào sau đây đúng?
A. \( 1<T<2 \)
B. \( \frac{1}{2}<T<\frac{2}{3} \)
C. \( -2<T<0 \)
D. \( 0<T<\frac{1}{2} \)
Hướng dẫn giải:
Đáp án D.
Giả sử: \({{\log }_{4}}a={{\log }_{6}}b={{\log }_{9}}(4a-5b)-1=t\)\(\Rightarrow \left\{ \begin{align} & a={{4}^{t}} \\ & b={{6}^{t}} \\ & 4a-5b={{9}^{t+1}} \\ \end{align} \right.\)
Khi đó: \( {{4.4}^{t}}-{{5.6}^{t}}={{9.9}^{t}}\Leftrightarrow 4{{\left( \frac{4}{9} \right)}^{t}}-5{{\left( \frac{6}{9} \right)}^{t}}=9 \)
\( \Leftrightarrow 4{{\left( \frac{2}{3} \right)}^{2t}}-5{{\left( \frac{2}{3} \right)}^{t}}-9=0\Leftrightarrow \left[ \begin{align} & {{\left( \frac{2}{3} \right)}^{t}}=\frac{9}{4}={{\left( \frac{2}{3} \right)}^{-2}} \\ & {{\left( \frac{2}{3} \right)}^{t}}=-1\text{(lo }\!\!{}^\text{1}\!\!\text{ i)} \\ \end{align} \right. \)
\( \Leftrightarrow t=-2\Rightarrow T=\frac{b}{a}={{\left( \frac{6}{4} \right)}^{t}}={{\left( \frac{3}{2} \right)}^{-2}}=\frac{4}{9}\in \left( 0;\frac{1}{2} \right) \).
Câu 7. Phương trình \( {{3}^{{{x}^{2}}}}{{.4}^{x+1}}-\frac{1}{{{3}^{x}}}=0 \) có hai nghiệm \( {{x}_{1}},\,{{x}_{2}} \). Tính \( T={{x}_{1}}.{{x}_{2}}+{{x}_{1}}+{{x}_{2}} \).
A. \( T=-{{\log }_{3}}4 \).
B. \( T={{\log }_{3}}4 \).
C. \( T=-1 \).
D. \( T=1 \).
Hướng dẫn giải:
Chọn C
Ta có: \( {{3}^{{{x}^{2}}}}{{.4}^{x+1}}-\frac{1}{{{3}^{x}}}=0\Leftrightarrow {{3}^{x(x+1)}}{{.4}^{x+1}}=1\Leftrightarrow \log \left( {{3}^{x(x+1)}}{{.4}^{x+1}} \right)=0 \)
\( \Leftrightarrow \log {{3}^{x(x+1)}}+\log {{4}^{x+1}}=0\Leftrightarrow x(x+1)\log 3+(x+1)\log 4=0 \)
\( \Leftrightarrow (x+1)\left( x\log 3+\log 4 \right)=0\Leftrightarrow \left[ \begin{align} & x=-1 \\ & x=-{{\log }_{3}}4 \\ \end{align} \right. \).
Do đó, \( T={{x}_{1}}.{{x}_{2}}+{{x}_{1}}+{{x}_{2}}={{\log }_{3}}4-(1+{{\log }_{3}}4)=-1 \).
