Trung Tâm Luyện Thi Đại Học
Bài tập Sử dụng sơ đồ Ven để giải toán
Câu 1. Lớp 10B1 có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10B1 là:
A. 9. B. 10. C. 18. C. 28.
Hướng dẫn giải:
Chọn B
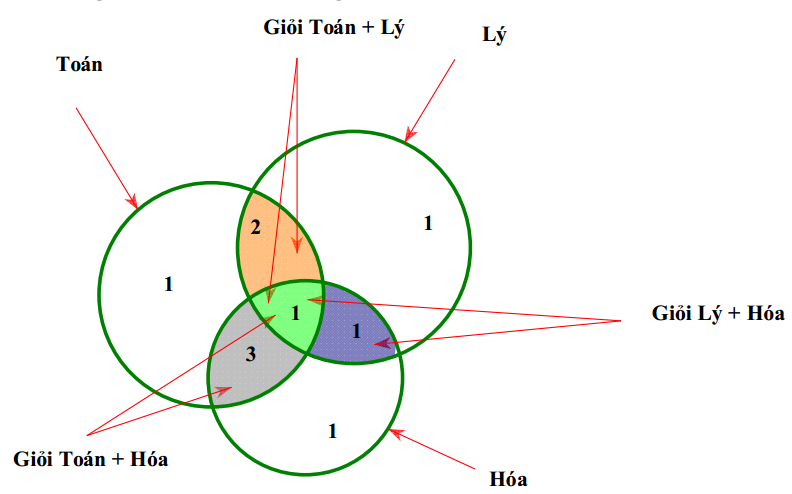
Ta dùng biểu đồ Ven để giải:
Nhìn vào biểu đồ, số học sinh giỏi ít nhất 1 trong 3 môn là: \( 1+2+1+3+1+1+1=10 \).
Câu 2. Lớp 10A có 40 học sinh trong đó có 10 bạn học sinh giỏi Toán,15 bạn học sinh giỏi Lý và 19 bạn không giỏi môn học nào trong hai môn Toán, Lý. Hỏi lớp 10A có bao nhiêu bạn học sinh vừa giỏi Toán vừa giỏi Lý?
A. 7. B. 10. C. 4. D. 17.
Hướng dẫn giải:
Chọn C
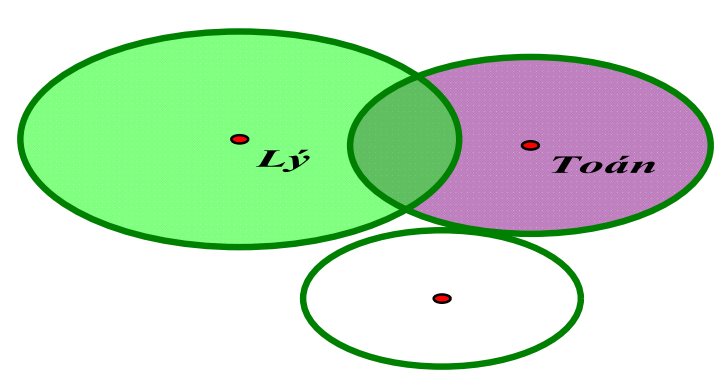
Số học sinh giỏi Toán hoặc Lý là: \( 40-19=21 \) (học sinh)
Số học sinh chỉ giỏi một môn Toán là: \( 21-10=11 \) (học sinh)
Số học sinh chỉ giỏi một môn Lý là: \( 21-15=6 \) (học sinh)
Số học sinh giỏi cả hai môn là: \( 21-11-6=4 \) (học sinh)
Câu 3. Trong kì thi học sinh giỏi cấp trường, lớp 11B1 có 15 học sinh giỏi Văn, 22 học sinh giỏi Toán. Tìm số học sinh giỏi V và Toán biết lớp 11B1 có 40 học sinh, và có 14 học sinh không đặt học sinh giỏi.
A. 4. B. 7. C. 11. D. 20.
Hướng dẫn giải:
Chọn C
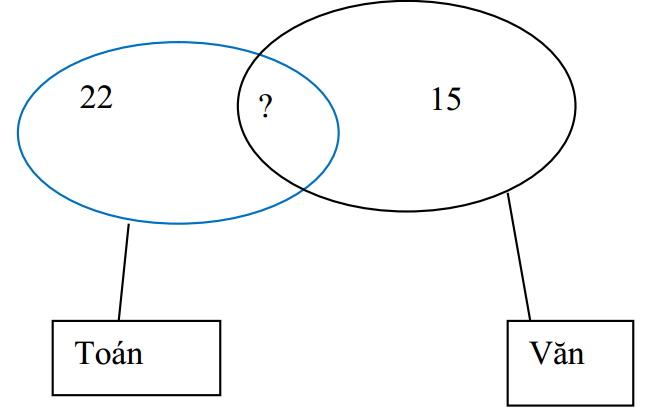
Số học sinh học giỏi ít nhất một trong hai môn Toán và Văn là: \( 40-14=26 \).
Số học sinh chỉ giỏi Toán mà không giỏi Văn (Phần Toán sau khi bỏ đi phần giao) là: \( 26-15=11 \).
Vậy số học sinh giỏi cả hai môn Toán và Văn (Phân giao nhau) là: \( 22-11=11 \).
Cách 2:
+ Số học sinh học giỏi ít nhất một trong hai môn Toán và Văn là: \( 40-14=26 \).
+ Số học sinh giỏi cả hai môn Toán và Văn là: \( 22+15-26=11 \).
Câu 4. Hội khỏe Phù Đổng của trường Trần Phú, lơp 10A có 45 học sinh, trong có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
A. 20. B. 45. C. 38. D. 21.
Hướng dẫn giải:
Chọn D
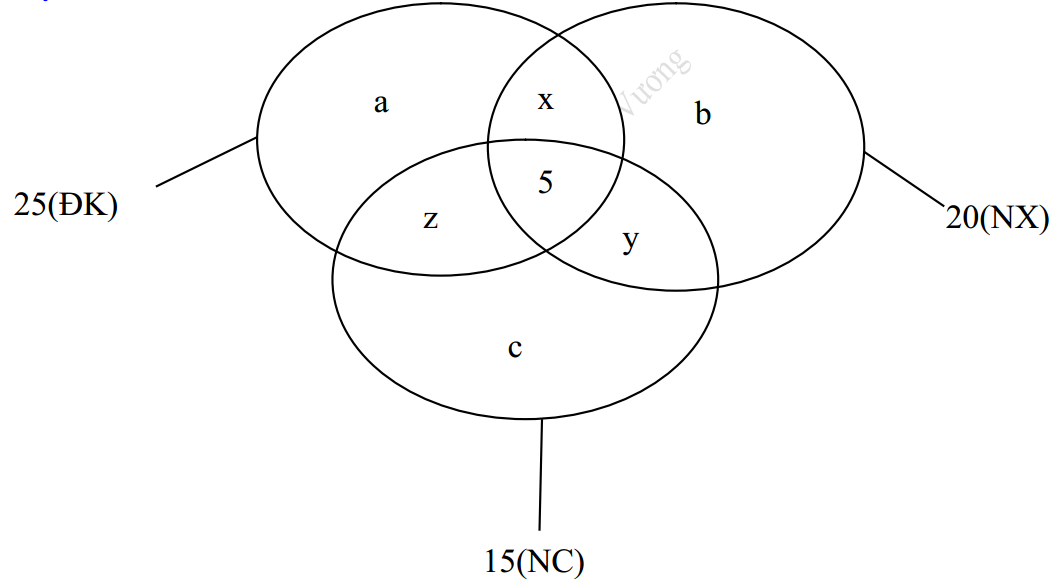
Gọi a, b, c theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
x là số học sinh chỉ thi hai môn điền kinh và nhảy xa.
y là số học sinh chỉ thi hai môn nhảy xa và nhảy cao.
z là số học sinh chỉ thi hia môn điền kinh và nhảy cao.
Số em thi ít nhất một môn là: \( 45-7=38 \).
Dựa vào biểu đồ Ven ta có hệ phương trình sau:
\( \left\{ \begin{align} & a+x+z+5=25\begin{matrix} {} & (1) \\\end{matrix} \\ & b+x+y+5=20\begin{matrix} {} & (2) \\\end{matrix} \\ & c+y+z+5=15\begin{matrix} {} & (3) \\\end{matrix} \\ & x+y+z+a+b+c+5=38\begin{matrix} {} & (4) \\\end{matrix} \\ \end{align} \right. \)
Cộng vế với vế của (1), (2), (3) ta có: \( a+b+c+2(x+y+z)+15=60 \) (5)
Từ (4), (5) ta có: \( a+b+c+2(38-5-a-b-c)+15=60\Leftrightarrow a+b+c=21 \).
Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.
Câu 5. Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
A. 11. B. 34. C. 1. D. 20.
Hướng dẫn giải:
Chọn D
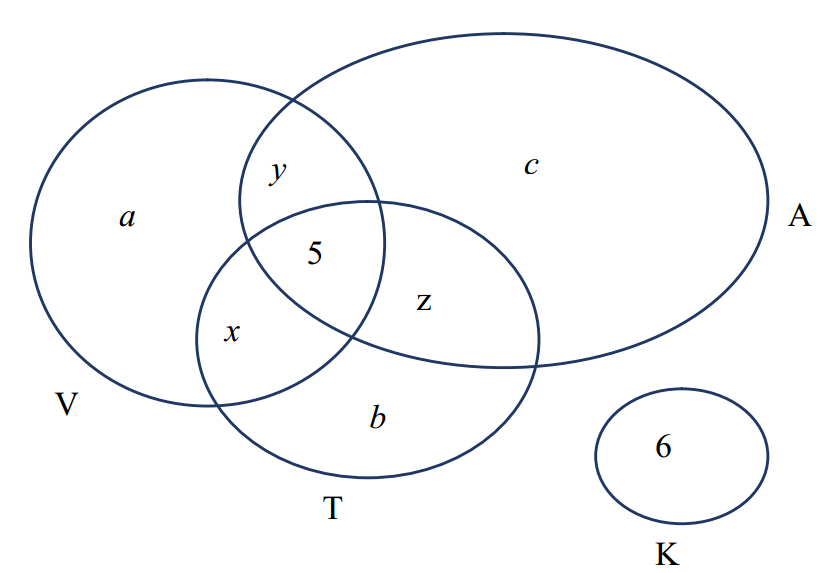
Trong lớp 10A, gọi T là tập hợp những em thích môn Toán; V là tập hợp những em thích môn Văn; A là tập hợp những em thích môn Tiếng Anh; K là tập hợp những em không thích môn nào.
Gọi a, b, c theo thứ tự là số học sinh chỉ thi môn Văn, Toán, Tiếng Anh.
x là số học sinh chỉ thích hai môn Văn và Toán.
y là số học sinh chỉ thích hai môn Văn và Tiếng Anh.
z là số học sinh chỉ thích hai môn Toán và Tiếng Anh.
Ta có biểu đồ Ven:
Từ biểu đồ Ven ta có hệ phương trình sau: \( \left\{ \begin{align} & a+x+y+5=25\begin{matrix} {} & (1) \\\end{matrix} \\ & b+x+z+5=20\begin{matrix} {} & (2) \\\end{matrix} \\ & c+y+z+5=18\begin{matrix} {} & (3) \\\end{matrix} \\ & x+y+z+a+b+c+5+6=45\begin{matrix} {} & (5) \\\end{matrix} \\ \end{align} \right. \)
Cộng vế với vế của (1), (2), (3) ta có: \( a+b+c+2(x+y+z)+15=63 \)
\(\Leftrightarrow a+b+c+2(x+y+z)=48\begin{matrix} {} & (4) \\\end{matrix}\)
Từ (4) và (5) ta có: \( \left\{ \begin{align} & a+b+c+2(x+y+z)=48 \\ & 2(x+y+z)+2(a+b+c)=68 \\ \end{align} \right.\Rightarrow a+b+c=20 \).
Vậy có 20 học sinh chỉ thích một trong ba môn trên.
Câu 6. Lớp 10A1 có 45 học sinh, trong đó có 17 bạn thích chơi bóng đá, 25 bạn thích chơi bóng rổ và 13 bạn không thích chơi môn bóng nào trong hai môn trên. Số học sinh thích chơi cả bóng đá và bóng rổ là:
A. 32. B. 42. C. 3. D. 10.
Hướng dẫn giải:
Chọn D
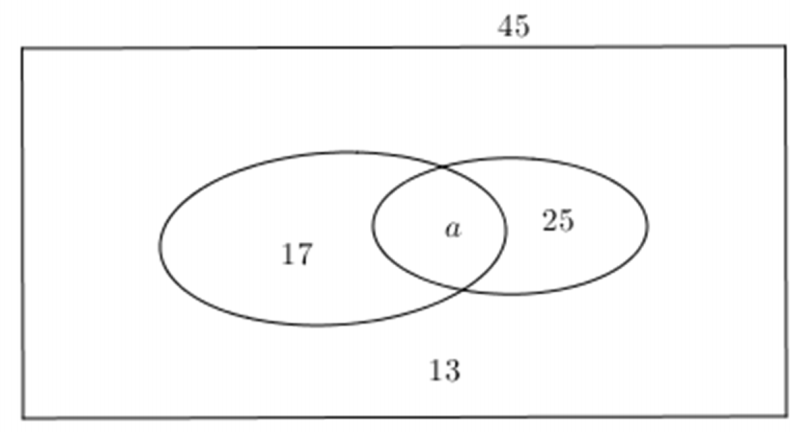
Biểu diễn tập hợp các bạn thích chơi bóng đá và các bạn thích chơi bóng rổ bằng hai đường kín; tập hợp các học sinh của lớp 10A1 bằng hình chữ nhật như hình bên dưới.
+ Gọi a là số học sinh thích chơi cả bóng đá và bóng rổ.
+ Dựa vào biểu đồ ta có: \( a+(17-a)+(25-a)+13=45\Leftrightarrow a=10 \).
Vậy có 10 học sinh thích chơi cả bóng đá và bóng rổ.
Câu 7. Trong lớp 10C2 có 16 học sinh giỏi môn Toán, 15 học sinh giỏi môn Lý và 11 học sinh giỏi môn Hóa. Biết rằng có 12 học sinh vừa giỏi môn Toán và Lý. 8 học sinh vừa giỏi môn Lý và Hóa. 9 học sinh vửa giỏi môn Toán và Hóa, trong đó có đúng 11 học sinh chỉ giỏi đúng 2 môn. Hỏi có bao nhiêu học sinh của lớp giỏi cả ba môn Toán, Lý. Hóa?
A. 4. B. 7. C. 5. D. 6.
Hướng dẫn giải:
Chọn D
Gọi x là số học sinh giỏi cả ba môn Toán, Lý và Hóa.
Số học sinh chỉ giỏi hai môn Toán và Lý là: \( 12-x \).
Số học sinh chỉ giỏi hai môn Lý và Hóa là: \( 8-x \).
Số học sinh chỉ giỏi hai môn Toán và Hóa là: \( 9-x \).
Ta có phương trình: \( 12-x+8-x+9-x=11\Leftrightarrow x=6 \).
Câu 8. Trong đợt khảo sát chất lượng, lớp 10C có 11 học sinh đạt điểm giỏi môn Toán, 8 học sinh đạt điểm giỏi môn Lý, 5 học sinh đạt điểm giỏi cả Toán và Lý, 4 học sinh đạt điểm giỏi cả Toán và Hóa, 2 học sinh đạt điểm giỏi cả Lý và Hóa, 1 học sinh đạt điểm giỏi cả 3 môn Toán, Lý, Hóa. Hỏi lớp 10C có bao nhiêu học sinh đạt điểm giỏi môn Hóa, biết trong lớp có 16 học sinh ít nhất một môn (Toán, Lý, Hóa)?
A. 7. B. 8. C. 5. D. 6
Hướng dẫn giải:
Chọn A
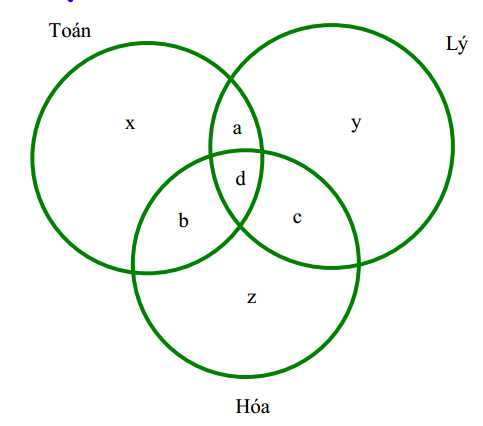
Gọi x là số học sinh chỉ giỏi Toán;
y là số học chỉ giỏi Lý;
z là số học sinh chỉ giỏi Hóa;
a là số học sinh chỉ giỏi Toán và Lý;
b là số học sinh chỉ giỏi Toán và Hóa;
c là số học sinh chỉ giỏi Hóa và Lý;
d là số học sinh giỏi cả 3 môn.
Theo đề ra ta có hệ phương trình: \( \left\{ \begin{align} & x+a+b+d=11\begin{matrix} {} & (1) \\\end{matrix} \\ & y+a+c+d=8\begin{matrix} {} & (2) \\\end{matrix} \\ & a+d=5\begin{matrix} {} & (3) \\\end{matrix} \\ & b+d=4\begin{matrix} {} & (4) \\\end{matrix} \\ & c+d=2\begin{matrix} {} & (5) \\\end{matrix} \\ & d=1\begin{matrix} {} & (6) \\\end{matrix} \\ & x+y+z+a+b+c+d=16\begin{matrix} {} & (7) \\\end{matrix} \\ \end{align} \right. \).
Từ phương trình \( (3),(4),(5),(6) \) ta được: \( a=4;\text{ }b=3;\text{ }c=1;\text{ }d=1 \).
Thay vào phương trình \( (1),\text{ }(2) \) ta được: \( x=3;\text{ }y=2 \).
Từ phương trình (7): \( x+y+z+a+b+c+d=16 \)
\( \Leftrightarrow z+b+c+d=16-x-y-a\Leftrightarrow z+b+c+d=7 \).
Vậy số học sinh đạt điểm giỏi môn Hóa là: \( z+b+c+d=7 \).
Câu 9. Trong một lớp học có 40 học sinh, trong đó có 30 học sinh đạt học sinh giỏi môn Toán, 25 học sinh đạt học sinh giỏi môn Văn. Biết rằng chỉ có 5 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả hai môn Toán và Văn. Hỏi có bao nhiêu học sinh chỉ học giỏi một môn trong hai môn Toán hoặc Văn?
A. 20. B. 15. C. 5. D. 10.
Hướng dẫn giải:
Chọn B
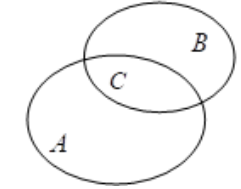
Gọi A là tập hợp các học sinh đạt học sinh giỏi môn Toán.
B là tập hợp các học sinh đạt học sinh giỏi môn Văn.
C là tập hợp các học sinh đạt học sinh giỏi cả hai môn Toán và Văn.
Số học sinh đạt học sinh giỏi môn Toán, Văn của lớp là: \( 40-5=35 \) (học sinh).
Theo sơ đồ Ven, ta có: \( A+B-C=35\Leftrightarrow 30+25-C=35\Leftrightarrow C=20 \).
Do vậy, ta có:
Số học sinh chỉ giỏi môn Toán là: \( A-C=30-20=10 \) (học sinh).
Số học sinh chỉ giỏi môn Văn là: \( B-C=25-20=5 \) (học sinh).
Nên số học sinh chỉ giỏi một trong hai môn Toán hoặc Văn là: \( 10+5=15 \) (học sinh).
Câu 10. Lớp 10A có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A là:
A. 9. B. 10. C. 18. C. 28.
Hướng dẫn giải:
Chọn B
+ Số học sinh chỉ giỏi môn Toán: \( 7-(3-1)-(4-1)-1=1 \) (học sinh).
+ Số học sunh chỉ giỏi môn Lý: \( 5-(3-1)-(2-1)-1=1 \) (học sinh).
+ Số học sinh chỉ giỏi môn Hóa: \( 6-(4-1)-(2-1)-1=1 \) (học sinh).
+ Số học sinh chỉ giỏi môn Toán, Lý không giỏi Hóa: \( 3-1=2 \) (học sinh).
+ Số học sinh chỉ giỏi môn Toán, Hóa không giỏi Lý: \( 4-1=3 \) (học sinh).
+ Số học sinh chỉ giỏi môn Lý, Hóa không giỏi Toán: \( 2-1=1 \) (học sinh).
Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10A là: \( 1+1+1+2+3+1+1=10 \) (học sinh).
Câu 11. Ba lớp 10A, 10B và 10C tham gia quyên góp sách cũ cho học sinh vùng lũ lụt. Tổng số sách mà ba lớp quyên được là 448 quyển. Trong đó, số sách lớp 10A nhiều hơn số sách lớp 10B là 32 quyển nhưng lại ít hơn số sách lớp 10C là 6 quyển. Hỏi lớp 10A quyên góp được bao nhiêu quyển sách cũ?
A. 126. B. 164. C. 158. D. 160.
Hướng dẫn giải:
Chọn C
Gọi số sách quyên góp được của các lớp 10A, 10B và 10C lần lượt là \( n(A),\text{ }n(B),\text{ }n(C) \).
Theo bài ra:
\( \left\{ \begin{align} & n(A)+n(B)+n(C)=448\begin{matrix} {} & (1) \\\end{matrix} \\ & n(B)=n(A)-32\begin{matrix} {} & (2) \\\end{matrix} \\ & n(C)=n(A)+6\begin{matrix} {} & (3) \\\end{matrix} \\ \end{align} \right. \).
Thay (2) và (3) vào (1), ta có: \( n(A)+n(B)+n(C)=448 \)
\( \Leftrightarrow n(A)+n(A)-32+n(A)+6=448\Leftrightarrow 3n(A)=474\Leftrightarrow n(A)=158 \) quyển.
Vậy số sách cũ lớp 10A quyên góp được là 158 quyển.
Câu 12. Một lớp có 40 học sinh, trong đó có 24 học sinh giỏi Toán, 20 học sinh giỏi Văn và 12 học sinh không giỏi môn nào trong hai môn Toán và Văn. Hỏi lớp đó có bao nhiêu học sinh giỏi cả hai môn Toán và Văn?
A. 16. B. 8. C. 4. D. 18.
Hướng dẫn giải:
Chọn A
Gọi A là tập hợp số học sinh giỏi môn Toán.
B là tập hợp số học sinh giỏi môn Văn.
Suy ra \( A\cup B \) là tập hợp số học sinh giỏi môn Toán hoặc Văn.
\( A\cap B \) là tập hợp số học sinh giỏi cả hai môn Toán và Văn.
+ Ta có: \( \left| A \right|=24,\text{ }\left| B \right|=20 \) và \( \left| A\cup B \right|=40-12=28 \).
+ Mà \( \left| A\cap B \right|=\left| A \right|+\left| B \right|-\left| A\cup B \right|=24+20-28=16 \).
Vậy số học sinh giỏi cả hai môn Toán và Văn là 16 học sinh.
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









