Trung Tâm Luyện Thi Đại Học
A. Định lí Thales
Thales là nhà toán học đầu tiên của Hi Lạp, ông sinh vào khoảng năm 624 – 547 trước Công nguyên tại thành phố Miletus trên bờ biển Địa Trung Hải. Ông còn là nhà triết học, thiên văn học, ông hướng dẫn cách xác định hướng đi biển theo chùm sao Tiểu Hùng Tinh trong một cuốn sách về hàng hải. Ông là một trong bảy nhà hiền triết nổi danh của Hi Lạp cổ đại, chính ông là người giải bài toán đo chiều cao Kim Tự tháp bằng phương pháp đồng dạng. Các tác phẩm của ông phần lớn đều bị thất lạc. Thales là người đưa ra năm định lý cơ bản của hình học.
- Góc chắn nửa đường tròn thì bằng một vuông.
- Đường kính chia đường tròn thành hai phần bằng nhau.
- Hai góc đáy của tam giác cân thì bằng nhau.
- Hai tam giác nếu có hai cặp góc và một cặp cạnh bằng nhau thì bằng nhau.
- Hai góc đối đỉnh thì bằng nhau.
Định lí Thales như một nền tảng cho sự ra đời của đồng dạng, từ đó người ta nhìn thấy bản chất của hình học vật thể, sự bất biến của phép chiếu song song.
Thales qua đời một cách đột ngột khi đang xem một thế vận hội. Trên mộ ông có khắc dòng chữ: “Nấm mồ này nhỏ bé làm sao! Nhưng quang vinh của con người này – ông vua của các nhà thiên văn mới vĩ đại làm sao!”
1. Định lí Thales thuận
Định lí. Nhiều đường thẳng song song cắt hai cát tuyến (đường thẳng) d, d’ thì tạo ra trên d, d’ các đoạn thẳng tương ứng tỉ lệ.
Nghĩa là: \(\left\{ \begin{align} & d\cap a=A,\text{ }d\cap b=B,\text{ }d\cap c=C \\ & {d}’\cap a={A}’,\text{ }{d}’\cap b={B}’,\text{ }{d}’\cap c={C}’ \\ & a\parallel b\parallel c \\ \end{align} \right.\Rightarrow \frac{AB}{{A}'{B}’}=\frac{BC}{{B}'{C}’}=\frac{CA}{{C}'{A}’}\).
Từ hệ thức trên ta còn viết dưới dạng các hệ thức:
\( \frac{AB}{BC}=\frac{{A}'{B}’}{{B}'{C}’};\text{ }\frac{AB}{CA}=\frac{{A}'{B}’}{{C}'{A}’};\text{ }\frac{BC}{CA}=\frac{{B}'{C}’}{{C}'{A}’} \).
Chứng minh:
(Cách chứng minh này ra đời thời Euclid)
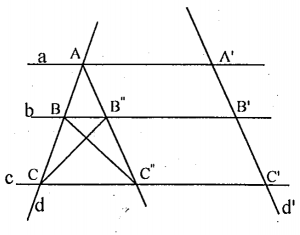
Từ A kẻ đường thẳng song song với d’ cắt b và c tại B’’ và C’’ \( \Rightarrow \) các tứ giác AA’B’B”, AA’C’C” là hình bình hành.
\( \Rightarrow A{B}”={A}'{B}’,\text{ }A{C}”={A}'{C}’ \).
Theo tính chất tỉ số diện tích hai tam giác, ta có: \( \frac{{{S}_{\Delta AB{B}”}}}{{{S}_{\Delta AC{B}”}}}=\frac{AB}{AC},\text{ }\frac{{{S}_{\Delta AB{B}”}}}{{{S}_{\Delta AB{C}”}}}=\frac{A{B}”}{A{C}”} \).
Mặt khác, \( B{B}’\parallel C{C}’\Rightarrow {{S}_{\Delta BC{B}”}}={{S}_{\Delta B{C}”{B}”}} \)
\( \Rightarrow {{S}_{\Delta AC{B}”}}={{S}_{\Delta AB{C}”}}\Rightarrow \frac{AB}{AC}=\frac{A{B}”}{A{C}”}\Rightarrow \frac{AB}{AC}=\frac{{A}'{B}’}{{A}'{C}’} \).
Euclid sinh ra ở thành Athena (khoảng năm 330 – 275 trước Công nguyên), vua Ai cập mời ông về làm việc ở chốn kinh kì Alexandria. Ông được mệnh danh là “Cha đẻ của Hình học”, bộ sách “Cơ sở” của ông đã đặt nền móng cho môn hình học cũng như toàn bộ toán học cổ đại. Bộ sách gồm 13 cuốn: sáu cuốn đầu gồm các kiến thức về hình học phẳng, ba cuốn tiếp theo có nội dụng số học được trình bày dưới dạng hình học, cuốn thứ mười gồm các phép dựng hình có liên quan đến đại số, 3 cuốn cuối cùng nói về hình học không gian. Euclid đã đưa ra 5 tiên đề làm cơ sở phát triển hình học ngày nay.
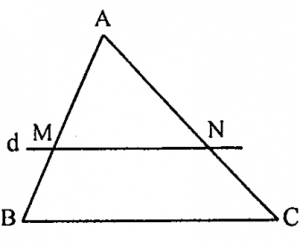
Hệ quả. Nếu đường thẳng d song song với cạnh BC của tam giác ABC (không qua đỉnh A) cắt các đường thẳng AB, AC tại M, N thì \( \frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC} \).
2. Định lí Thales đảo
Định lí. Ba đường thẳng a, b, c trong đó \( a\parallel b \), cắt hai đường thẳng d, d’, định ra trên d, d’ những đoạn thẳng tương ứng tỉ lệ thì \( a\parallel c \).
Tức là \( \left\{ a,b,c;a\parallel c;\frac{AB}{{A}'{B}’}=\frac{BC}{{B}'{C}’}=\frac{CA}{{C}'{A}’}\Rightarrow a\parallel c \right\} \).
Chứng minh:
Giả sử \( a\cancel{\parallel }c \), từ C dựng đường thẳng c song song với a cắt d’ tại C”, theo định lí Thales thuận \( \Rightarrow \frac{AB}{{A}'{B}’}=\frac{BC}{{B}'{C}”} \).
Kết hợp giả thiết suy ra: \( \frac{BC}{{B}'{C}’}=\frac{BC}{{B}'{C}”}\Rightarrow {B}'{C}’={B}'{C}”\Rightarrow {C}’\equiv {C}”\Rightarrow a\parallel c \).
3. Các đường thẳng đồng quy cắt hai đường thẳng song song
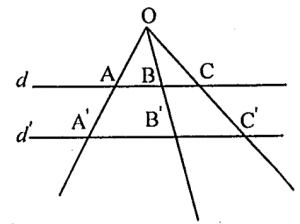
Định lí. Nếu ba đường thẳng a, b, c đồng quy tại O cắt hai đường thẳng song song d, d’ không đi qua O thì chúng định ra trên d, d’ hai bộ ba đoạn thẳng tỉ lệ.
Nếu a, b, c đồng quy tại O và \( d\parallel {d}’ \).
\( \Rightarrow \frac{AB}{{A}'{B}’}=\frac{BC}{{B}'{C}’}=\frac{CA}{{C}'{A}’} \) hoặc \( \frac{OA}{O{A}’}=\frac{OB}{O{B}’}=\frac{OC}{O{C}’} \).
B. Bài tập có hướng dẫn giải
Câu 1. Cho tam giác ABC, O là điểm trong tam giác. AO, BO, CO cắt các cạnh BC, CA, AB lần lượt tại D, E, F. Qua O kẻ đường thẳng song song với BC cắt DE, DF tại N và M. Chứng minh rằng \( OM=ON \).
Hướng dẫn giải:
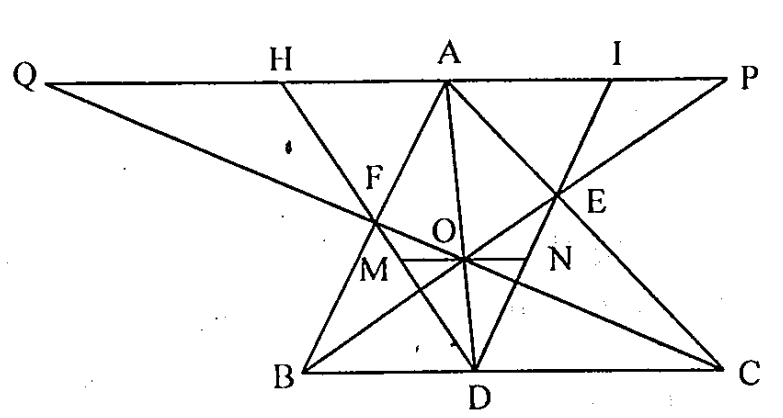
Qua A kẻ đường thẳng song song với BC cắt BO, CO, DE, DF lần lượt tại P, Q, I, H.
Theo định lí Thales, ta có: \( \frac{AQ}{BC}=\frac{AH}{BD},\text{ }\frac{BC}{AP}=\frac{DC}{AI} \).
Nhân hai đẳng thức \( \Rightarrow \frac{AQ}{AP}=\frac{AH}{BD}.\frac{DC}{AI} \).
Mặt khác: \( \frac{AQ}{AP}=\frac{DC}{DB}\Rightarrow \frac{AQ}{AP}=\frac{DC}{DB}=\frac{AH}{BD}.\frac{DC}{AI} \).
\(\Rightarrow \frac{AH}{AI}=1\Rightarrow AH=AI,\text{ }\Delta DHI\) có DA là trung tuyến \( \Rightarrow OM=ON \).
Câu 2. Cho tam giác ABC, M là điểm trên cạnh BC. Qua B, C dựng các đường thẳng song song với AM cắt AC, AB lần lượt tại P, Q. Chứng minh rằng \( \frac{1}{AM}=\frac{1}{PB}+\frac{1}{QC} \).
Hướng dẫn giải:
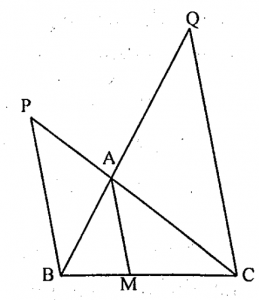
Theo giả thiết \( AM\parallel PB\parallel QC \), theo định lí Thales
\( \Rightarrow \frac{AM}{PB}=\frac{CM}{CB} \) và \( \frac{AM}{QC}=\frac{BM}{BC} \), cộng hai vế ta có: \( \frac{AM}{PB}+\frac{AM}{QC}=\frac{CM}{CB}+\frac{BM}{BC}=\frac{BM+MC}{BC}=\frac{BC}{BC}=1 \)
\( \Rightarrow \frac{1}{AM}=\frac{1}{PB}+\frac{1}{QC} \).
Câu 3. Cho ba đoạn thẳng có độ dài là a, b, c. Dựng đoạn thẳng x thỏa mãn \( \frac{1}{x}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \).
Hướng dẫn giải:
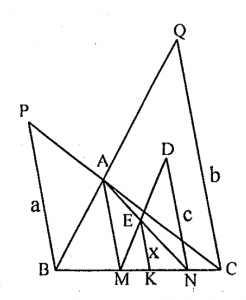
Áp dụng Ví dụ 2 ta dựng đoạn thẳng y thỏa mãn \( \frac{1}{y}=\frac{1}{a}+\frac{1}{b} \);
Với đoạn thẳng BC tùy ý, từ B và C dựng hai đoạn thẳng song song thỏa mãn \( BP=a \) và \( CQ=b \);
+ PC và QB cắt nhau tại A, từ A kẻ \( AM\parallel PB \) \( \Rightarrow \frac{1}{AM}=\frac{1}{a}+\frac{1}{b} \);
+ N là điểm tùy ý trên BC, qua N dựng đường thẳng \( ND\parallel PB \) và \( ND=c \);
+ AN cắt MD tại E, từ E kẻ \( EK\parallel PB \)
Theo Ví dụ 2 \( \Rightarrow EK=x \) (Bạn đọc tự chứng minh)
Câu 4. Cho tam giác ABC ( \( AB=AC \)), kéo dài BC về phía C lấy điểm M. Đường thẳng d qua M cắt cạnh AB, AC lần lượt tại P và Q. Chứng minh rằng \( \frac{BM}{BP}-\frac{CM}{CQ} \) không phụ thuộc vào vị trí của M và đường thẳng d.
Hướng dẫn giải:
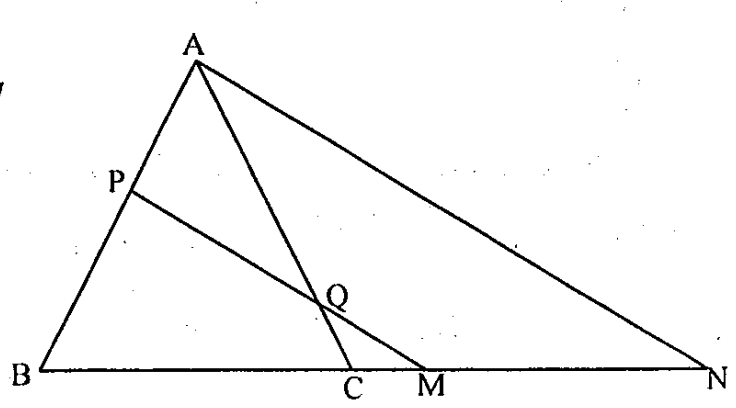
Qua A dựng đường thẳng song song với d cắt BC tại N, theo định lí Thales ta có: \( \frac{BM}{BP}=\frac{BN}{BA} \) và \( \frac{CM}{CQ}=\frac{CN}{CA} \), trừ hai vế ta có:
\( \frac{BM}{BP}-\frac{CM}{CN}=\frac{BN}{BA}-\frac{CN}{CA}=\frac{BC}{AB} \).
\( \frac{BC}{AB} \) không phụ thuộc vị trí M và đường thẳng d \( \Rightarrow \frac{BM}{BP}-\frac{CM}{CQ} \) không phụ thuộc vị trí M và đường thẳng d.
Câu 5. Trên đường trung tuyến AD của tam giác ABC, lấy điểm E bất kì, đường thẳng BE cắt AC tại M và đường thẳng CE cắt AB tại N. Chứng minh rằng \( MN\parallel BC \).
Hướng dẫn giải:
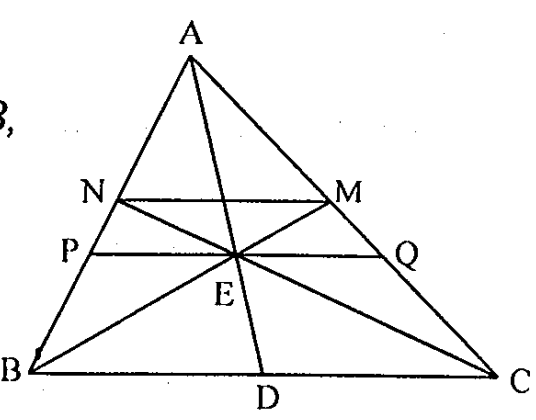
Từ E dựng đường thẳng song song với BC cắt AB, AC lần lượt tại P và Q. Theo định lí Thales suy ra:
\( \frac{AP}{AB}=\frac{AE}{AD}=\frac{PE}{BD} \) và \( \frac{AE}{AD}=\frac{AQ}{AC}=\frac{ED}{DC} \).
\( \Rightarrow \frac{PE}{BD}=\frac{EQ}{DC},\text{ }BD=DC\Rightarrow PE=EQ \).
\( \Rightarrow \frac{NP}{NB}=\frac{NE}{NC}=\frac{PE}{BC} \) và \( \frac{ME}{MB}=\frac{MQ}{MC}=\frac{EQ}{BC} \)
\( \Rightarrow \frac{NE}{NC}=\frac{ME}{MB}\Rightarrow MN\parallel BC \).
Từ kết quả này ta suy ra bài toán: Chứng minh rằng trong một hình thang, trung điểm hai cạnh đáy, giao điểm hai đường chéo, giao điểm hai đường thẳng chứa hai cạnh bên nằm trên một đường thẳng.
Kết quả này như một hệ quả được sử dụng chứng minh cho nhiều bài toán khác.
Câu 6. Cho tam giác ABC ( \( AB>AC \)), D là trung điểm BC, phân giác góc \( \widehat{A} \) cắt cạnh BC tại E. Từ C kẻ đường thẳng vuông góc với AE cắt AE, AD lần lượt tại F và G. Chứng minh rằng DF song song với AB, GE song song với AC. Từ đó suy ra DF đi qua trung điểm của GE.
Hướng dẫn giải:
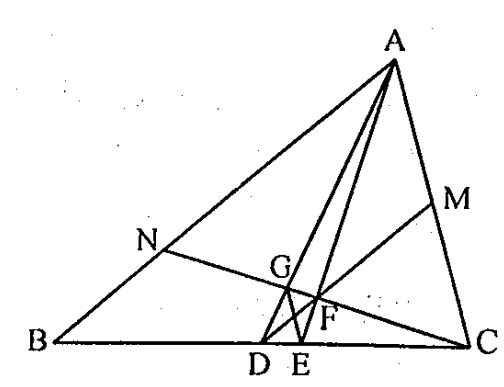
Kéo dài DF cắt AC tại M, CF cắt AB tại N, AE là phân giác góc \( \widehat{A} \), \( CN\bot AE\Rightarrow \Delta CAN \) là tam giác cân.
\( \Rightarrow AN=AC\Rightarrow FC=FN \).
Theo giả thiết \( DB=DC\Rightarrow \frac{CF}{FN}=\frac{CD}{DB} \).
\( \Rightarrow DM\parallel AB\Rightarrow MA=MC \), \( DF\parallel AB\Rightarrow DM \) là trung tuyến của \( \Delta ADC \).
Theo Ví dụ 5 \( \Rightarrow GE\parallel AC\Rightarrow DF \) đi qua trung điểm EG.
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









