Trung Tâm Luyện Thi Đại Học
B. Bài tập có hướng dẫn giải (tiếp theo)
Câu 6. Gọi I là tâm đường tròn nội tiếp tam giác ABC, đường thẳng AI cắt đường tròn ngoại tiếp tam giác ABC tại D, E là điểm trên cung \( \overset\frown{BDC} \), F trên cạnh BC thỏa mãn \( \widehat{BAF}=\widehat{CAE}<\frac{1}{2}\widehat{BAC} \), gọi G là trung điểm IF. Chứng minh rằng giao điểm của DG và EI nằm trên đường tròn ngoại tiếp tam giác ABC.
Hướng dẫn giải:
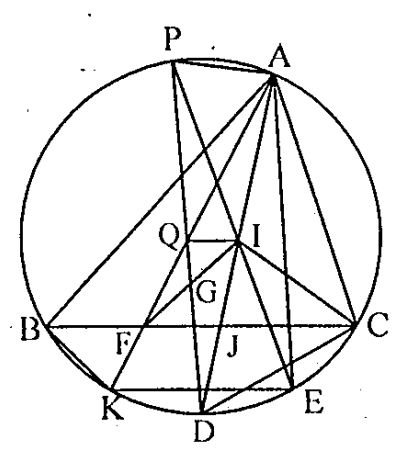
Gọi P là giao điểm của EI cắt đường tròn ngoại tiếp tam giác ABC, đường thẳng AI cắt BC tại J; AF cắt đường tròn ngoại tiếp \( \Delta ABC \) tại K, cắt DP tại Q.
Theo giả thiết \( \widehat{BAF}=\widehat{CAE}<\frac{1}{2}\widehat{BAC}\Rightarrow \overset\frown{CE}=\overset\frown{BK}\Rightarrow CE=BK\Rightarrow BC\parallel KE \);
AD là phân giác góc \( \widehat{A}\Rightarrow \widehat{KAD}=\widehat{DPE} \).
\( \Rightarrow APQI \) nội tiếp \( \Rightarrow \widehat{AQI}=\widehat{API}=\widehat{AKE}\Rightarrow QI\parallel KE\Rightarrow QI\parallel KE\parallel BC \).
\( \Rightarrow \frac{QF}{QA}=\frac{IJ}{IA} \), AI cắt BC tại J, I là tâm đường tròn nội tiếp \( \Rightarrow \frac{JI}{IA}=\frac{CJ}{CA} \);
\( \widehat{BCD}=\widehat{BAD}=\widehat{CAD}\Rightarrow \Delta DCJ\backsim \Delta DAC \) (g.g).
\( \Rightarrow \frac{CJ}{AC}=\frac{DC}{DA} \), kết hợp \( DI=DC\Rightarrow \frac{DC}{DA}=\frac{ID}{AD} \).
\( \frac{FQ}{QA}=\frac{JI}{AI}=\frac{CJ}{AC}=\frac{DC}{AD}=\frac{ID}{AD} \) (*)
Theo Menelaus với \( \Delta AIF \) cát tuyến PQD, giả sử PQD cắt FI tại G’, ta có: \( \frac{QA}{QF}.\frac{{G}’F}{{G}’I}.\frac{DI}{DA}=1 \), kết hợp \( (*)\Rightarrow \frac{{G}’F}{{G}’I}=1\Rightarrow {G}’F={G}’I\Rightarrow G\equiv {G}’ \).
\( \Rightarrow DG \) và EI cắt nhau trên đường tròn ngoại tiếp \( \Delta ABC \).
Câu 7. Cho tứ giác ABCD và I, J trung điểm của AD và BC. Gọi G, E là trọng tâm tam giác ABC và ABD. Chứng minh rằng DG, CE, IJ đồng quy, từ đó suy ra GE song song với CD.
Hướng dẫn giải:
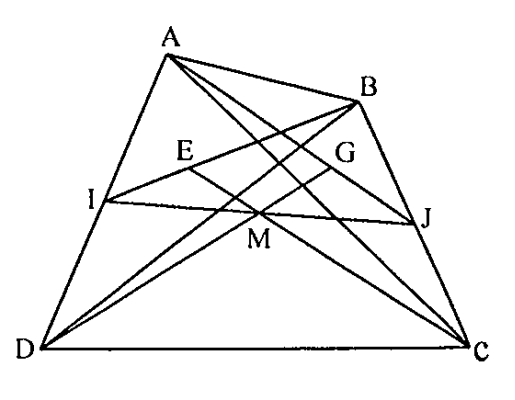
G là trọng tâm của \( \Delta ABC\Rightarrow AG=2GJ \).
Áp dụng định lí Menelaus với \( \Delta AIJ \), đường thẳng DG cắt tại M \( \Rightarrow \frac{DA}{DI}.\frac{MI}{MJ}.\frac{GJ}{GA}=1 \).
\( IA=ID\Rightarrow DA=2DI\Rightarrow 2.\frac{MI}{MJ}.\frac{1}{2}=1 \).
\( \Rightarrow MI=MJ \), E là trọng tâm \( \Delta ABD \), hoàn toàn tương tự
\( \Rightarrow CE \) đi qua trung điểm của IJ \( \Rightarrow \) ba đường thẳng DG, CE, IJ đồng quy.
Áp dụng định lí Menelaus với \( \Delta ADG \), ứng với ba điểm M, I, J thẳng hàng
\( \Rightarrow \frac{IA}{ID}.\frac{MD}{MG}.\frac{JG}{JA}=1\Rightarrow \frac{MD}{MG}.\frac{1}{3}=1\Rightarrow \frac{MD}{MG}=3 \), tương tự \( \Rightarrow \frac{MC}{ME}=3 \).
\( \Rightarrow \frac{MD}{MG}=\frac{MC}{ME} \), theo định lí Thales thì EG song song với CD.
Câu 8. Cho tam giác ABC, gọi I là trung điểm của BC. Qua I kẻ đường thẳng d1 cắt CA, AB tại M, N và đường thẳng d2 cắt cạnh CA, AB tại P, Q. Đường thẳng PN cắt cạnh BC tại E và đường thẳng QM cắt cạnh BC tại F. Chứng minh \( IE=IF \).
Hướng dẫn giải:
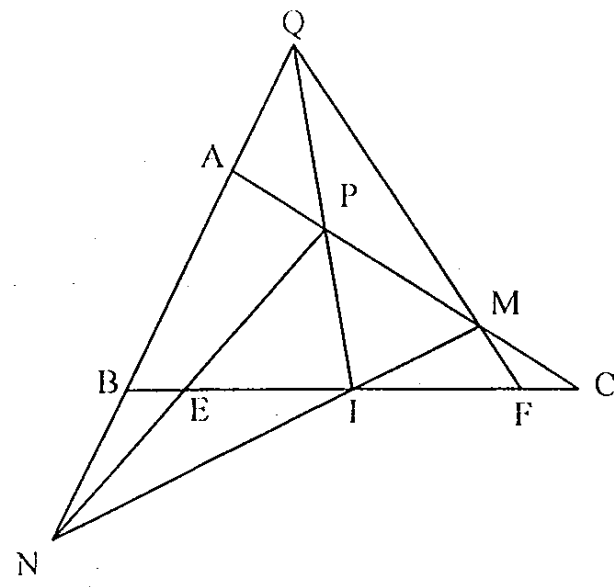
Áp dụng định lí Menelaus trong \( \Delta ABC \) với cát tuyến MNI, ta có:
\( \frac{IB}{IC}.\frac{MC}{MA}.\frac{NA}{NB}=1\Rightarrow \frac{MC}{MA}.\frac{NA}{NB}=1 \).
Với cát tuyến PQI, ta có:
\( \Rightarrow \frac{IC}{IB}.\frac{QB}{QA}.\frac{PA}{PC}=1\Rightarrow \frac{QB}{QA}.\frac{PA}{PC}=1 \)
\( \Rightarrow \frac{MC}{MA}.\frac{NA}{NB}=\frac{QB}{QA}.\frac{PA}{PC}\Rightarrow \frac{PC}{PA}.\frac{NA}{NB}=\frac{QB}{QA}.\frac{MA}{MC} \) (*)
Tương tự đối với cát tuyến NEP và QMF:
\( \frac{EB}{EC}.\frac{PC}{PA}.\frac{NA}{NB}=1 \) và \( \frac{FC}{FB}.\frac{QB}{QA}.\frac{MA}{MC}=1 \)
\( \Rightarrow \frac{EB}{EC}.\frac{PC}{PA}.\frac{NA}{NB}=\frac{FC}{FB}.\frac{QB}{QA}.\frac{MA}{MC} \) kết hợp với (*), ta có:
\( \frac{EB}{EC}=\frac{FC}{FB}\Rightarrow \frac{EB}{EB+EC}=\frac{FC}{FB+FC}\Rightarrow \frac{EB}{BC}=\frac{FC}{BC} \)
\( \Rightarrow EB=FC\Rightarrow IE=IF \).
Câu 9. Cho hai đoạn thẳng AC và BD cắt nhau tại E. M trên đoạn AB và N trên đoạn CD sao cho M, E, N thẳng hàng. Chứng minh \( MN\le \max \{AC,BD\} \).
Hướng dẫn giải:
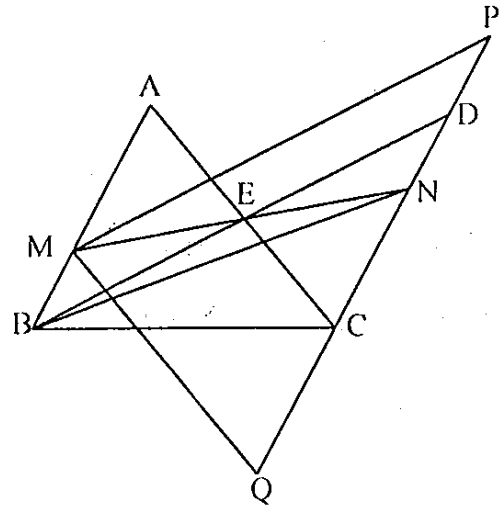
+ Trường hợp \( AB\parallel CD \).
Từ M kẻ đường thẳng song song với BD cắt CD tại P và đường thẳng song song với AC cắt CD tại Q.
\( \Rightarrow \) Tứ giác MPDB và MACQ là hình bình hành.
\( \Rightarrow BD=MP \) và \( AC=MQ \).
Ta chứng minh: \( MN\le \max \{MP,MQ\} \).
\( N\in CD\Rightarrow MN\le \max \{MP,MQ\} \)
\( \Rightarrow MN\le \max \{AC,BD\} \).
+ Trường hợp AB không song song với CD.
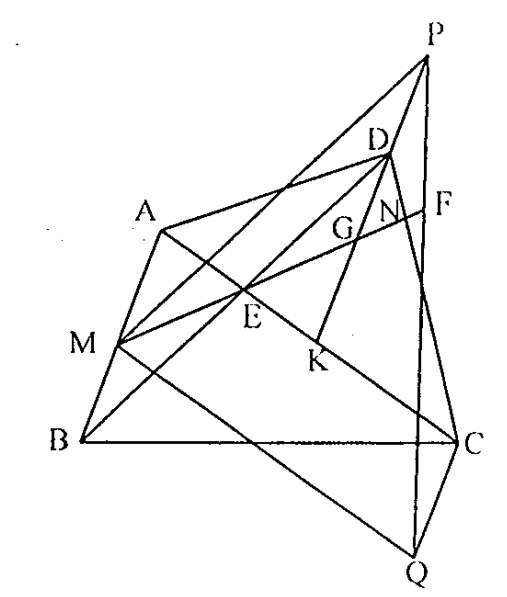
Giả sử \( \widehat{A}+\widehat{D}>{{180}^{O}}\Rightarrow \widehat{B}+\widehat{C}<{{180}^{O}} \).
Từ D kẻ đường thẳng song song với AB cắt MN, AC tại G và K.
Áp dụng định lí Menelaus đối với \( \Delta DKC với ba điểm E, G, N \Rightarrow \frac{GK}{GD}.\frac{ND}{NC}.\frac{EC}{EK}=1 \).
\( \Rightarrow \frac{GK}{GD}.\frac{ND}{NC}=\frac{EK}{EC}<1\Rightarrow \frac{GK}{GD}<\frac{NC}{ND} \) (1)
\( AB\parallel DK\Rightarrow \frac{GK}{GD}=\frac{MA}{MB} \) (2)
Kẻ \( CQ\parallel AB \) và \( MQ\parallel AC \), \( DP\parallel AB \) và \( MP\parallel BD \).
\( \Rightarrow \) Tứ giác AMQC và BMPD là hình bình hành.
\( \Rightarrow AC=MQ,\text{ }AM=CQ \) và \( BD=MP,BM=DP\Rightarrow CQ\parallel AB\parallel DP \), gọi I là giao điểm của PQ với CD.
\( \Rightarrow \frac{CI}{ID}=\frac{CQ}{DP}=\frac{MA}{MB} \), từ (1) và (2) \( \frac{NC}{ND}>\frac{IC}{ID}=\frac{MA}{MB} \).
\( \Rightarrow DI\ge DN \), giao điểm MN cắt PQ tại F \( \Rightarrow MN\le MF \).
\( \Rightarrow MN<\max \{MP,MQ\}=\max \{BD,AC\} \).
Câu 10. Cho hình thang ABCD ( \( AB\parallel CD,\text{ }AB<CD \)). M, N trên AB và CD sao cho \( \frac{AM}{MB}=\frac{DN}{NC} \), P và Q trên MN sao cho \(\widehat{DPC}=\widehat{ABC}\) và \( \widehat{AQB}=\widehat{BCD} \). Chứng minh rằng P, Q, B, C nằm trên một đường tròn.
Hướng dẫn giải:
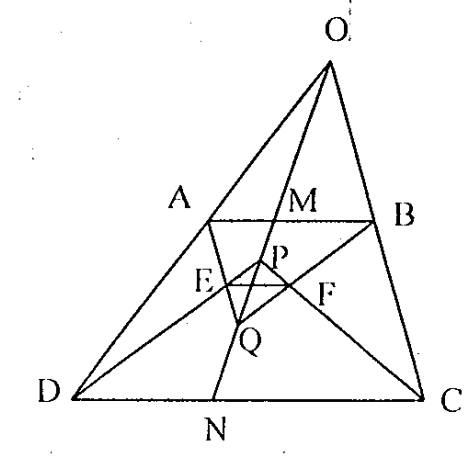
Gọi E là giao điểm AQ và DP, và F là giao điểm BQ và CP \(\Rightarrow \widehat{EPF}=\widehat{ABC}\) và \(\widehat{FQE}=\widehat{BCD}\).
Ta có: \( \widehat{ABC}+\widehat{BCD}={{180}^{O}}\Rightarrow PFQE \) là tứ giác nội tiếp.
Áp dụng định lí Menelaus đối với \( \Delta DOP \) với đường thẳng AQ và \( \Delta COP \) với đường thẳng BQ:
\( \frac{AD}{AO}.\frac{QO}{QP}.\frac{EP}{ED}=1 \) và \( \frac{BC}{BO}.\frac{QO}{QP}.\frac{FP}{FC}=1 \) \( \Rightarrow \frac{AD}{AO}.\frac{QO}{QP}.\frac{EP}{ED}=\frac{BC}{BO}.\frac{QO}{QP}.\frac{FP}{FC} \).
Do \( \frac{AD}{AO}=\frac{BC}{BO}\Rightarrow \frac{EP}{ED}=\frac{FP}{FC}\Rightarrow EF\parallel CD\parallel AB \).
\( \Rightarrow \widehat{ABC}=\widehat{ABQ}+\widehat{QBC}=\widehat{EFQ}+\widehat{QBC}=\widehat{EPQ}+\widehat{QBC} \).
\( \widehat{ABC}=\widehat{DPC}=\widehat{EPQ}+\widehat{QPC}\Rightarrow \widehat{QBC}=\widehat{QPC} \).
\( \Rightarrow P,Q,C,B \) nằm trên một đường tròn.
Câu 11. Cho tứ giác ABCD, đường thẳng d cắt AB, BC, CA, AD lần lượt tại M, N, P, Q. Chứng minh \( \frac{MA}{MB}.\frac{NB}{NC}.\frac{PC}{PD}.\frac{QD}{QA}=1 \).
Hướng dẫn giải:
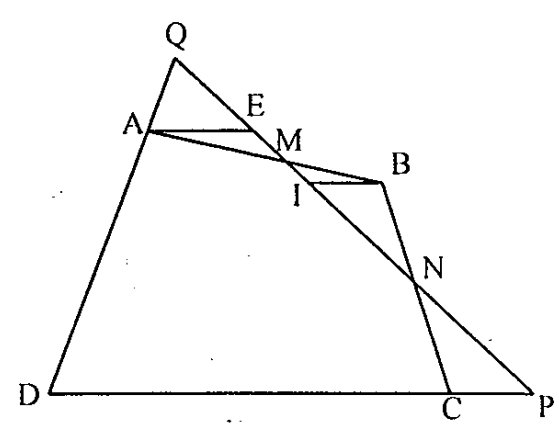
Từ A, B kẻ các đường thẳng song song với CD cắt MN tại E và F, theo định lí Thales, ta có:
\( \frac{MA}{MB}=\frac{AE}{IB},\text{ }\frac{NB}{NC}=\frac{BI}{CP},\text{ }\frac{QD}{QA}=\frac{PD}{AE} \).
\( \Rightarrow \frac{MA}{MB}.\frac{NB}{NC}.\frac{QD}{QA}=\frac{AE}{IB}.\frac{BI}{CP}.\frac{PD}{AE}=\frac{PD}{CP} \)
\( \Rightarrow \frac{MA}{MB}.\frac{NB}{NC}.\frac{PC}{PD}.\frac{QD}{QA}=1 \).
Chú ý,áp dụng cho tứ giác chỉ có chiều thuận.
Câu 12. Cho tam giác ABC ( \( AC>AB \)), đường phân giác góc A và đường trung trực BC cắt nhau tại D, gọi H, K là hình chiếu của D trên AC và AB. Chứng minh rằng cạnh BC, đường trung trực BC và HK đồng quy.
Hướng dẫn giải:
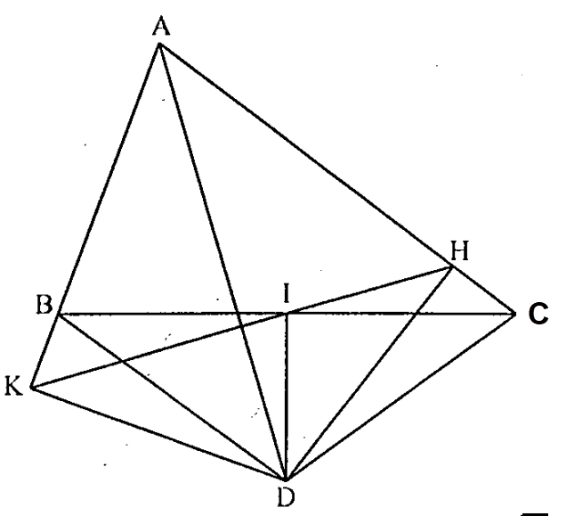
AD là phân giác góc \( \widehat{A} \) \( \Rightarrow DK=DH \), D nằm trên trung trực BC \( \Rightarrow DB=DC \).
\( \Rightarrow \Delta DHC=\Delta DKB\Rightarrow CH=BK \) và \( AH=AK \).
Gọi giao điểm của HK và BC là I, áp dụng định lí Menelaus.
\( \Rightarrow \frac{IB}{IC}.\frac{HC}{HA}.\frac{KA}{KB}=1\Rightarrow IB=IC\Rightarrow \) (đpcm).
Câu 13. Cho tam giác vuông ABC (vuông tại A), đường tròn tâm B bán kính BA và đường tròn tâm C, bán kính CA cắt nhau tại D (D khác A), BC cắt chuyển động tròn tâm (B) tại E, F và cắt đường tròn tâm (C) tại M, N. Đường thẳng DM cắt AE tại P, DQ cắt AN tại Q.Kéo dài DM cắt đường tròn (B) tại I, DF cắt đường tròn (C) tại H. Chứng minh: \( \frac{IP}{IM}.\frac{HF}{HQ}=\frac{AB}{AC} \).
Hướng dẫn giải:
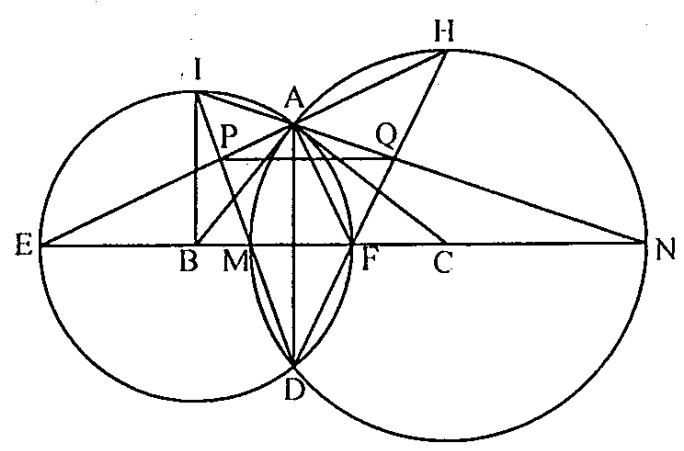
\( \widehat{AEN}+\widehat{ANE}=\frac{1}{2}\left( \widehat{B}+\widehat{C} \right)={{45}^{O}} \)
\( \widehat{AEF}=\widehat{ADF},\text{ }\widehat{ANM}=\widehat{ADM} \)
\( \Rightarrow \widehat{IDF}=\widehat{IDA}+\widehat{ADF}={{45}^{O}} \)
\( \Rightarrow \widehat{IBF}={{90}^{O}}\Rightarrow IB\bot EF\Rightarrow \widehat{IAE}={{45}^{O}} \).
\( \Rightarrow I,A,N \) thẳng hàng, tương tự E, A, H thẳng hàng.
\( \Rightarrow \widehat{EAN}={{135}^{O}}\Rightarrow \) Tứ giác APDQ nội tiếp.
\( \Rightarrow \widehat{APQ}=\widehat{ADQ}=\widehat{AEC}\Rightarrow PQ\parallel EN\Rightarrow \frac{AP}{AQ}=\frac{AE}{AN} \).
Áp dụng định lí Menelaus với \( \Delta PEM \), cát tuyến IAN: \( \frac{IP}{IM}.\frac{NM}{NE}.\frac{AE}{AP}=1 \).
Tương tự với \( \Delta QFN\Rightarrow \frac{HF}{HQ}.\frac{AQ}{AN}.\frac{EN}{EF}=1 \).
Nhân hai đẳng thức trên ta được: \( \frac{IP}{IM}.\frac{HF}{HQ}.\frac{NM.AE.AQ}{AP.EF.AN}=1\Rightarrow \frac{IP}{IM}.\frac{HF}{HQ}=\frac{EF}{NM}=\frac{AB}{AC} \).
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









