Trung Tâm Luyện Thi Đại Học
Định lí Thales (tiếp theo)
Câu 7. Cho tứ giác ABCD, đường chéo AC, BD cắt nhau tại O. Chứng minh rằng ABCD là hình thang khi và chỉ khi \( OA.OD=OB.OC \).
Hướng dẫn giải:
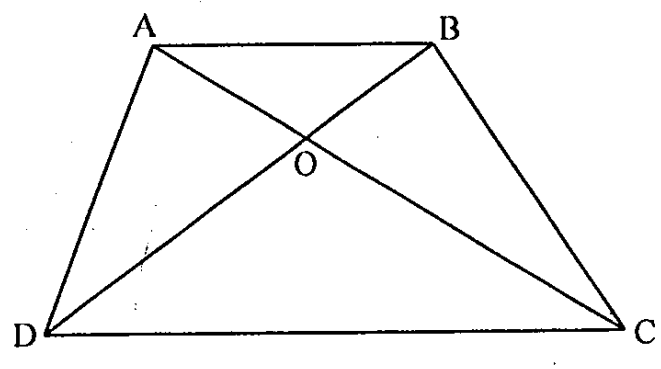
ABCD là hình thang, giả sử \( AB\parallel CD \)
\( \Rightarrow \frac{OA}{OC}=\frac{OB}{OD}\Rightarrow OA.OD=OB.OC \).
Ngược lại: Giả sử ta có \( OA.OD=OB.OC \)
\( \Rightarrow \frac{OA}{OC}=\frac{OB}{OD},\text{ }\widehat{AOB}=\widehat{DOC}\Rightarrow \Delta AOB\backsim \Delta COD \)
\( \Rightarrow \widehat{BAO}=\widehat{DCO}\Rightarrow AB\parallel CD\Rightarrow ABCD \) là hình thang.
Câu 8. Cho tam giác nhọn ABC, đường phân giác AD, gọi M và B là hình chiếu của D trên AC và AB. Giao điểm của BM và CN là P. Chứng minh rằng AP vuông góc với BC.
Hướng dẫn giải:
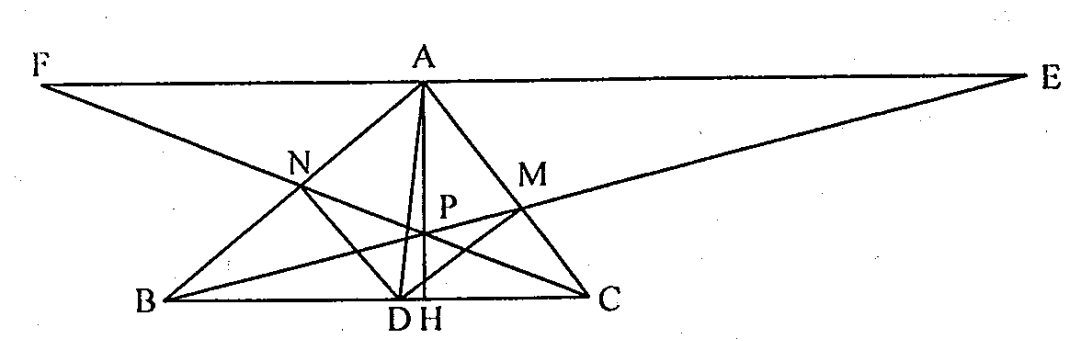
Qua A kẻ đường thẳng d song song với BC, đường thẳng BM, CN cắt d tại E và F, gọi H là giao điểm của AP và BC. Theo định lí Thales, ta có:
\( \frac{HC}{HB}=\frac{AF}{AE},\text{ }\frac{AM}{CM}=\frac{AE}{BC}\Rightarrow AM=\frac{AE.CM}{BC},\text{ }\frac{AN}{BN}=\frac{AF}{BC}\Rightarrow AN=\frac{AF.BN}{BC} \);
\( DM\bot AC,\text{ }DN\bot AB,\text{ }\widehat{BAD}=\widehat{CAD}\Rightarrow \Delta AMD=\Delta AND\Rightarrow AN=AM \).
\( \Rightarrow AE.CM=AF.BN\Rightarrow \frac{CM}{BN}=\frac{AF}{AE}\Rightarrow \frac{HC}{HB}=\frac{CM}{BN} \) (*)
Kẻ \( AK\bot BC\Rightarrow \Delta DMC \) và \( \Delta AKC \) là hai tam giác vuông có góc \( \widehat{C} \) chung.
\( \Rightarrow \Delta DMC\backsim \Delta AKC\Rightarrow \frac{CD}{CA}=\frac{CM}{CK} \), tương tự \( \frac{BD}{AB}=\frac{BN}{BK} \).
AD là phân giác \( \Rightarrow \frac{CD}{CA}=\frac{BD}{AB}\Rightarrow \frac{CM}{CK}=\frac{BN}{BK}\Rightarrow \frac{CM}{BN}=\frac{CK}{BK} \), kết hợp (*)
\( \Rightarrow K\equiv H\Rightarrow AP\bot BC \).
Câu 9. Cho tứ giác ABCD, O là giao điểm hai đường chéo AC, BD. Gọi M, N là trung điểm của BD và AC, H là điểm đối xứng của O qua MN, đường thẳng qua H và song song với MN cắt AD, BC, BD, AC lần lượt tại P, Q, E, F. Chứng minh rằng \( PE=QF \).
Hướng dẫn giải:
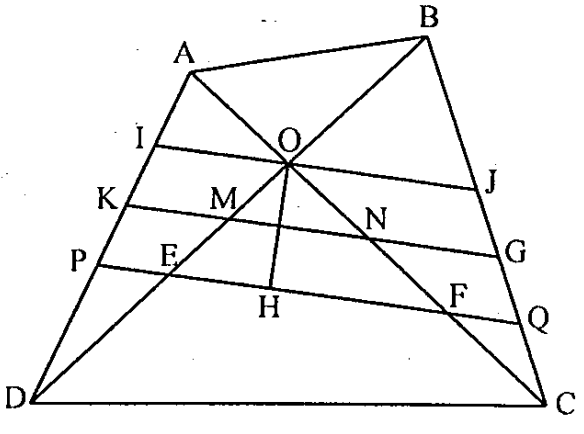
Theo giả thiết H đối xứng với O qua MN \( \Rightarrow OM=ME \) và \( MB=MD \) \( \Rightarrow OB=ED \), tương tự \( FC=OA \);
Qua O kẻ \( IJ\parallel MN \), theo định lí Thales \( \Rightarrow \frac{PE}{OI}=\frac{DE}{DO}=\frac{OB}{DO}\Rightarrow PE=\frac{OB.OI}{DO} \).
Tương tự \( QF=\frac{OA.OJ}{CO} \);
MN cắt AD và BC tại K và G.
\( \Rightarrow \frac{KM}{IO}=\frac{DM}{DO}=\frac{BD}{2DO},\text{ }\frac{KN}{IO}=\frac{AN}{AO}=\frac{AC}{2AO} \).
Trừ hai đẳng thức \( \Rightarrow \frac{MN}{IO}=\frac{1}{2}\left( \frac{AC}{AO}-\frac{BD}{DO} \right) \).
Tương tự \( \frac{MN}{JO}=\frac{1}{2}\left( \frac{BD}{BO}-\frac{AC}{CO} \right) \).
Để chứng minh \( PE=QF\Leftrightarrow \frac{OB.OI}{DO}=\frac{OA.OJ}{CO}\Leftrightarrow \frac{OB.MN}{DO.OJ}=\frac{OA.MN}{CO.OI} \)
\( \Leftrightarrow \frac{OB}{DO}\left( \frac{BD}{BO}-\frac{AC}{CO} \right)=\frac{OA}{CO}\left( \frac{AC}{AO}-\frac{BD}{DO} \right)\Leftrightarrow \frac{BD}{DO}-\frac{OB.AC}{DO.CO}=\frac{AC}{CO}-\frac{OA.BD}{CO.DO} \)
\( \Leftrightarrow \frac{BD}{DO}+\frac{OA.BD}{CO.DO}=\frac{AC}{CO}+\frac{OB.AC}{DO.CO} \), hai vế cho kết quả \( \frac{AC.BD}{DO.CO} \).
Ví dụ này ngoài vận dụng định lí Thales còn đòi hỏi biến đổi và kẻ thêm hình.
Câu 10. Cho tam giác ABC. Qua đỉnh A bờ AB kẻ tia Ax và tia Ay thỏa mãn \( Ax\parallel BC \) và tia Ax nằm trong góc \( \widehat{CAy} \), từ C kẻ đường thẳng d cắt Ax tại D và Ay tại E, đường thẳng BD cắt AC tại F. Chứng minh rằng đường thẳng EF đi qua điểm cố định không phụ thuộc đường thẳng d.
Hướng dẫn giải:
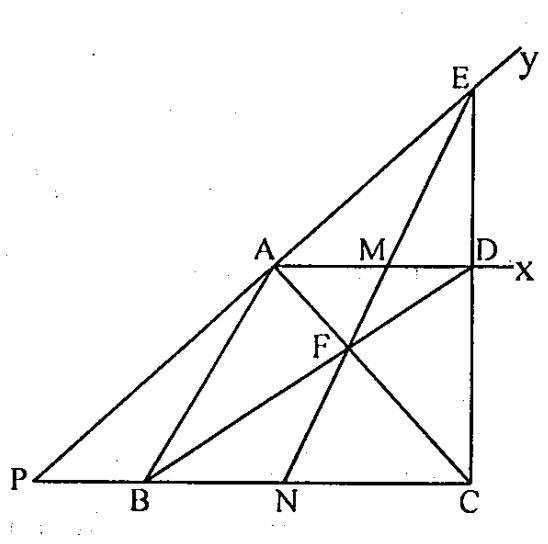
Kéo dài tia Ay cắt BC tại P, EF cắt AD tại M và BC tại N.
Theo giả thiết \( Ax\parallel BC \), theo định lí Thales, ta có:
\( \frac{MA}{MD}=\frac{NP}{NC} \) và \( \frac{MA}{MD}=\frac{NC}{NB} \) \( \Rightarrow \frac{NP}{NC}=\frac{NC}{NB}\Rightarrow \frac{NP}{NP+NC}=\frac{NC}{NC+NB} \)
\( \Rightarrow \frac{NP}{CP}=\frac{NC}{BC}\Rightarrow \frac{CP-CN}{CP}=\frac{NC}{BC} \)
\( \Rightarrow \frac{NC}{BC}+\frac{NC}{CP}=1\Rightarrow NC\left( \frac{1}{BC}+\frac{1}{CP} \right)=1 \)
\( \Rightarrow CN=\frac{BC.CP}{BC+CP} \), tia Ay cố định \( \Rightarrow P \) cố định \( \Rightarrow CP \) không đổi.
\( \Rightarrow \) Biểu thức \( \frac{BC.CP}{BC+CP} \) có giá trị không đổi \( \Rightarrow CN \) không đổi.
\( \Rightarrow \) Đường thẳng luôn đi qua điểm cố định N, không phụ thuộc đường thẳng d.
Câu 11. Cho tam giác ABC, M là điểm trên cạnh BC. Chứng minh rằng \( MA.BC<MB.CA+MC.AB \).
Hướng dẫn giải:
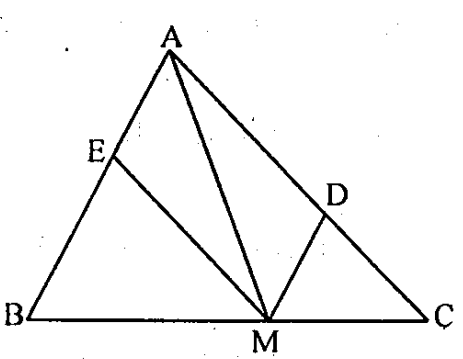
Từ M kẻ các đường thẳng song song với AB, AC cắt cạnh AC, AB lần lượt tại D và E \( \Rightarrow \) Tứ giác AEMD là hình bình hành \( \Rightarrow MD=AE \).
Theo định lí Thales \( \frac{MB}{BC}=\frac{ME}{CA}\Rightarrow MB=\frac{BC.ME}{CA} \), tương tự \( MC=\frac{BC.MD}{AB} \).
Thay MB và MC vào biểu thức \( MB.CA+MC.AB \), ta có:
\( MB.CA+MC.AB=\frac{BC.ME}{CA}.CA+\frac{BC.MD}{AB}.AB=BC(ME+MD)=BC(ME+AE) \)
\( ME+AE>MA\Rightarrow MB.CA+MC.AB>BC.MA \).
Câu 12. Cho bộ ba điểm thẳng hàng theo thứ tự \( ({{A}_{1}},{{A}_{2}},{{A}_{3}}) \) và \( ({{B}_{1}},{{B}_{2}},{{B}_{3}}) \) thỏa mãn \( \frac{{{A}_{1}}{{A}_{2}}}{{{A}_{1}}{{A}_{3}}}=\frac{{{B}_{1}}{{B}_{2}}}{{{B}_{1}}{{B}_{3}}}=k \). Trên \( {{A}_{1}}{{B}_{1}},{{A}_{2}}{{B}_{2}},{{A}_{3}}{{B}_{3}} \) lần lượt lấy các điểm \( {{C}_{1}},{{C}_{2}},{{C}_{3}} \) thỏa mãn \( \frac{{{C}_{1}}{{A}_{1}}}{{{C}_{1}}{{B}_{1}}}=\frac{{{C}_{2}}{{A}_{2}}}{{{C}_{2}}{{B}_{2}}}=\frac{{{C}_{3}}{{A}_{3}}}{{{C}_{3}}{{B}_{3}}} \). Chứng minh rằng \( {{C}_{1}},{{C}_{2}},{{C}_{3}} \) thẳng hàng và \( \frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}{{C}_{3}}}=k \).
Hướng dẫn giải:
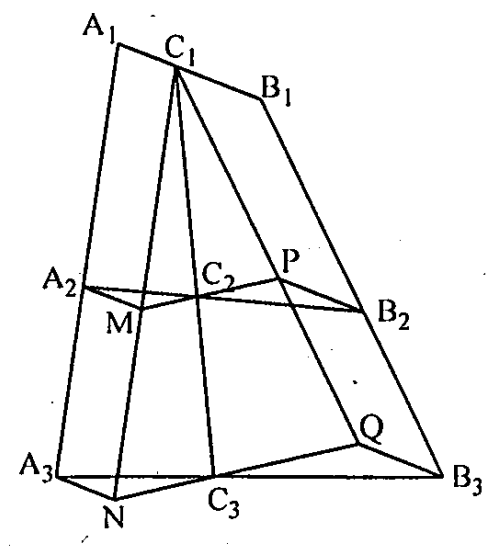
Từ C1 kẻ đường thẳng song song với A1A3 trên đó lấy các điểm M, N sao cho A2M và A3N song song với A1C1, tương tự \( {{B}_{1}}{{B}_{3}}\parallel {{C}_{1}}Q \) và \( P{{B}_{2}}\parallel {{C}_{1}}{{B}_{1}} \), \( Q{{B}_{3}}\parallel {{C}_{1}}{{B}_{1}} \).
\( \Rightarrow {{A}_{1}}{{C}_{1}}M{{A}_{2}} \) là hình bình hành \( \Rightarrow {{A}_{1}}{{A}_{2}}={{C}_{1}}M \) và \( {{A}_{1}}{{A}_{3}}={{C}_{1}}N \).
\( \Rightarrow \frac{{{A}_{1}}{{A}_{2}}}{{{A}_{1}}{{A}_{3}}}=\frac{{{C}_{1}}M}{{{C}_{1}}N}=k \);
Hoàn toàn tương tự \( \frac{{{C}_{1}}P}{{{C}_{1}}Q}=\frac{{{B}_{1}}{{B}_{2}}}{{{B}_{1}}{{B}_{3}}}=k \)
\( \Rightarrow \frac{{{C}_{1}}M}{{{C}_{1}}N}=\frac{{{C}_{1}}P}{{{C}_{1}}Q}\Rightarrow MP\parallel NQ \);
Với cách dựng trên \( \Rightarrow {{A}_{1}}{{C}_{1}}={{A}_{2}}M={{A}_{3}}N \) và \( {{B}_{1}}{{C}_{1}}={{B}_{2}}P={{B}_{3}}Q \), \( {{A}_{2}}M\parallel {{B}_{2}}P \).
Kết hợp giả thiết \(\Rightarrow \frac{{{A}_{2}}M}{{{B}_{2}}P}=\frac{{{C}_{2}}{{A}_{2}}}{{{C}_{2}}{{B}_{2}}},\text{ }\widehat{{{C}_{2}}{{A}_{2}}M}=\widehat{{{C}_{2}}{{B}_{2}}P}\Rightarrow \Delta M{{A}_{2}}{{C}_{2}}\backsim \Delta P{{B}_{2}}{{C}_{2}}\).
\( \Rightarrow \widehat{{{A}_{2}}{{C}_{2}}M}=\widehat{{{B}_{2}}{{C}_{2}}P}\Rightarrow M,{{C}_{2}},P \) thẳng hàng.
Hoàn toàn tương tự \( \Rightarrow \frac{{{A}_{3}}N}{{{B}_{3}}Q}=\frac{{{A}_{3}}{{C}_{3}}}{{{B}_{3}}{{C}_{3}}}\Rightarrow N,{{C}_{3}},Q \) thẳng hàng và \( \frac{{{C}_{2}}M}{{{C}_{2}}P}=\frac{{{C}_{3}}N}{{{C}_{3}}Q} \)
\( \Rightarrow {{C}_{1}},{{C}_{2}},{{C}_{3}} \) thẳng hàng và \( \frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}{{C}_{3}}}=\frac{{{A}_{1}}{{A}_{2}}}{{{A}_{1}}{{A}_{3}}}=k \).
Câu 13. Cho đa giác ABCDE, thỏa mãn \( \widehat{BAC}=\widehat{CAD}=\widehat{DAE} \) và \( \widehat{ABC}=\widehat{ACD}=\widehat{ADE} \). Đường thẳng BD cắt CE tại M. Chứng minh rằng AM đi qua trung điểm CD.
Hướng dẫn giải:
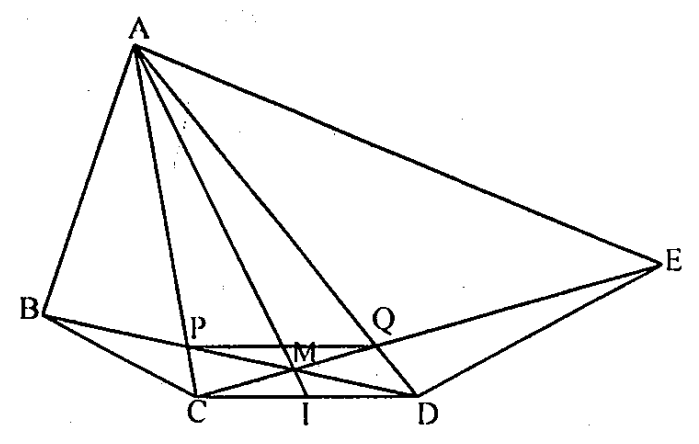
Theo giả thiết \( \widehat{BAC}=\widehat{CAD}=\widehat{DAE} \) và \( \widehat{ABC}=\widehat{ACD}=\widehat{ADE} \).
\( \Rightarrow \Delta ABC,\text{ }\Delta ACD,\text{ }\Delta ADE \) đồng dạng (g.g)
\( \Rightarrow \frac{AB}{AC}=\frac{AC}{AD}=\frac{AD}{AE} \) (1)
Giả sử BD cắt AC tại P, CE cắt AD tại Q.
Từ giả thiết \( \widehat{BAD}=\widehat{BAC}+\widehat{CAD}=\widehat{CAD}+\widehat{DAE}=\widehat{CAE} \)
\( \Rightarrow \widehat{BAD}=\widehat{CAE}\Rightarrow \Delta ABD\backsim \Delta ACE \) (c.g.c).
AP là phân giác của \( \widehat{BAD} \), AQ là phân giác \( \widehat{CAE} \) \( \Rightarrow \frac{AB}{AC}=\frac{AP}{AQ} \).
Kết hợp (1) \( \Rightarrow \frac{AP}{AQ}=\frac{AC}{AD}\Rightarrow \frac{AP}{AC}=\frac{AQ}{AD} \), theo định lý Thales đảo \( \Rightarrow PQ\parallel CD \).
\( \Rightarrow PQCD \) là hình thang \( \Rightarrow \) theo tính chất hình thang AM đi qua trung điểm CD
\( \Rightarrow IC=ID \).
Câu 14. Cho tam giác ABC nội tiếp đường tròn (O), AD là phân giác của tam giác, M là điểm thay đổi trên AD, P và Q là hình chiếu của M trên AB và AC, I là trung điểm BC, H là hình chiếu của I trên PQ. Chứng minh rằng MH luôn đi qua điểm cố định khi M thay đổi trên AD.
Hướng dẫn giải:
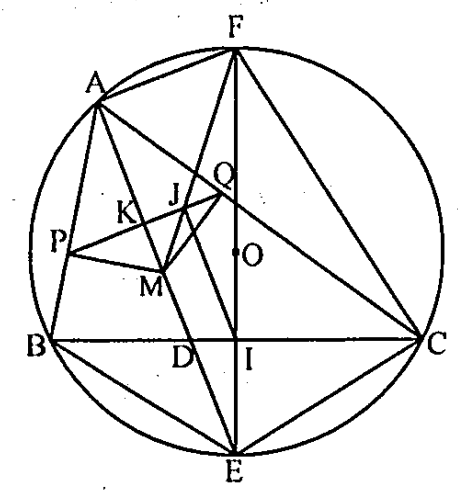
AD cắt đường tròn (O) tại E \( \Rightarrow EC=EB \)
\( \Rightarrow EI \) là đường thẳng chứa một đường kính của đường tròn (O) cố định, đường kính này cắt (O) tại F.
\( \Rightarrow F \) là điểm cố định.
Giả sử MF cắt PQ tại J. Theo giả thiết ta có \( \widehat{PAM}=\widehat{QAM} \), \(MP\bot AB,\text{ }MQ\bot AC\)
\( \Rightarrow AM\bot PQ \).
Gọi K là giao điểm AM và PQ, EF là đường kính.
\( \Rightarrow \widehat{ECF}={{90}^{O}},\widehat{EFC}=\widehat{EAC} \) (chắn cung \( \overset\frown{CE} \))
\( \Rightarrow \Delta AQM\backsim \Delta FCE \) (g.g) \( \Rightarrow \frac{FI}{IE}=\frac{AK}{KM} \) (1)
Mặt khác EF là đường kính nên \( AE\bot AF\Rightarrow AF\parallel PQ\Rightarrow \frac{AK}{KM}=\frac{FJ}{JM} \) (2)
Từ (1) và (2) \( \Rightarrow \frac{FI}{IE}=\frac{FJ}{JM} \), theo định lí Thales đảo \( \Rightarrow IJ\parallel AD \).
\( \Rightarrow IJ\bot PQ\Rightarrow J\equiv H\Rightarrow MH \) luôn đi qua F là điểm cố định.
Câu 15. Cho tứ giác ABCD, AB không song song với CD. Đường tròn (C1) qua A, B và tiếp xúc với CD tại P, đường tròn (C2) qua C, D và tiếp xúc với AB tại Q, (C1) và (C2) cắt nhau tại E và F. Chứng minh rằng EF đi qua trung điểm của PQ khi và chỉ khi BC song song với AD.
Hướng dẫn giải:
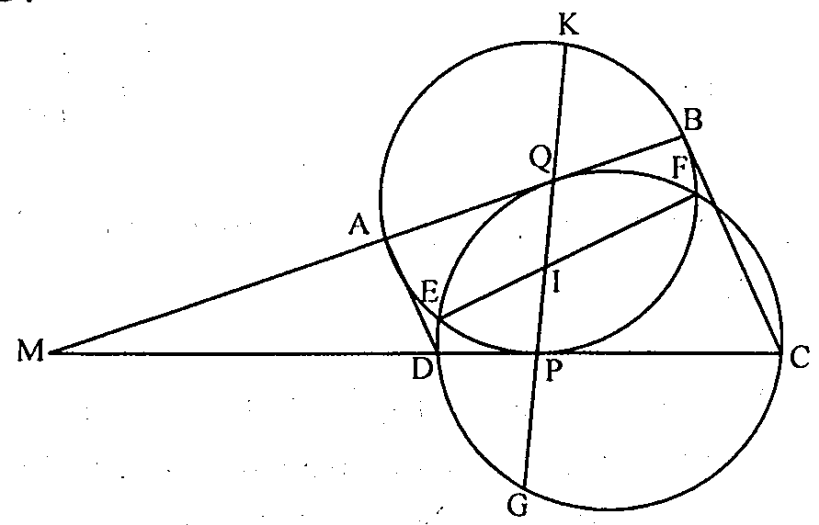
Gọi I là giao điểm của EF và PQ, đường thẳng PQ cắt đường tròn (C1) và đường tròn (C2) thứ tự tại K và G.
Theo giả thiết AB không song song với CD nên AB và CD giao nhau, gọi giao điểm là M.
Theo hệ thức đường tròn \( \Rightarrow M{{P}^{2}}=MA.MB \) và \( M{{Q}^{2}}=MC.MD \) (1)
Mặt khác, ta có: \( IE.IF=IP.IK=IQ.IG\Rightarrow IP(IQ+QK)=IQ(IP+PG) \)
\( \Rightarrow IP.QK=IQ.PG\Rightarrow IP=IQ\Leftrightarrow QK=PG\Leftrightarrow PQ.QK=PQ.PG \)
\( \Leftrightarrow QA.QB=PD.PC \) (2)
Ta có: \( AQ=MQ-MA,\text{ }QB=MB-MQ,DP=MP-MD \) và \( PC=MC-MP \).
Từ (2) và kết hợp (1) suy ra: \( (MB-MQ)(MQ-MA)=(MP-MD)(MC-MP) \)
\( \Leftrightarrow MB.MQ-MQ.MB-M{{Q}^{2}}+MQ.MA=MP.MC-M{{P}^{2}}-MD.MC+MD.MP \)
\( \Leftrightarrow MB.MQ+MQ.MA=MP.MC+MD.MP \)
\( \Leftrightarrow MQ(MB+MA)=MP(MC+MD)\Leftrightarrow M{{Q}^{2}}{{(MB+MA)}^{2}}=M{{P}^{2}}{{(MC+MD)}^{2}} \)
\( \Leftrightarrow MD.MC{{(MA+MB)}^{2}}=MA.MB{{(MC+MD)}^{2}} \)
\( \Leftrightarrow {{(MA.MC-MD.MB)}^{2}}=0\Leftrightarrow MA.MC=MD.MB\Leftrightarrow \frac{MA}{MB}=\frac{MD}{MC}\Leftrightarrow BC\parallel AD \).
Câu 16. Cho tam giác nhọn ABC, gọi (O1), (O2) là tâm đường tròn bàng tiếp của tam giác ứng với góc \( \widehat{B} \) và \( \widehat{C} \). Đường tròn (O1) tiếp xúc với cạnh BC, AB, CA tại M, N, E đường tròn (O2) tiếp xúc với cạnh BC, AC, AB tại P, Q, F; đường thẳng MN và PQ cắt nhau tại D. Chứng minh rằng AD vuông góc với BC.
Hướng dẫn giải:
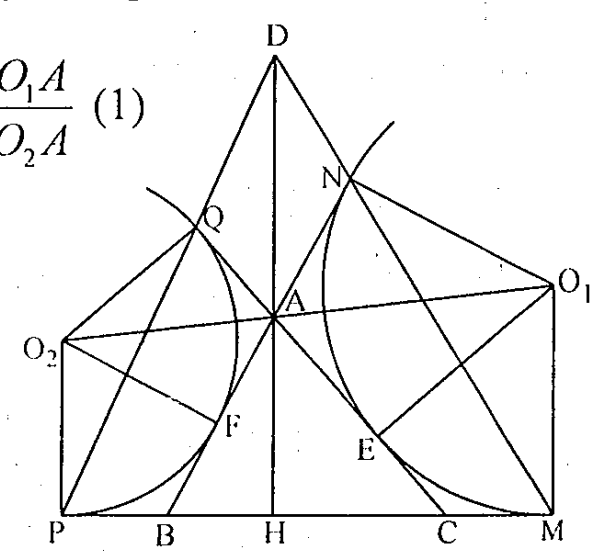
Theo giả thiết đường tròn (O1) tiếp xúc AC tại E, AB tại N suy ra \( {{O}_{1}}N\bot AB \), \( {{O}_{1}}E\bot AC \) \( \Rightarrow \widehat{{{O}_{1}}AN}=\widehat{{{O}_{1}}AE} \);
Đường tròn (O2) tiếp xúc AB tại F và AC tại Q suy ra \( {{O}_{2}}Q\bot AC \), \( {{O}_{2}}F\bot AB \).
\( \Rightarrow \widehat{{{O}_{2}}AQ}=\widehat{{{O}_{2}}AF}\Rightarrow \widehat{{{O}_{1}}AN}=\widehat{{{O}_{2}}AF}\Rightarrow {{O}_{1}},A,{{O}_{2}} \) thẳng hàng.
\( \Rightarrow \Delta {{O}_{2}}QA\backsim \Delta {{O}_{1}}NA \) (g.g) \( \Rightarrow \frac{AN}{AQ}=\frac{{{O}_{1}}A}{{{O}_{2}}A} \) (1)
Theo giả thiết \( {{O}_{1}}M\bot BC,\text{ }{{O}_{2}}P\bot BC \).
\( \Rightarrow \frac{PH}{MH}=\frac{{{S}_{DPH}}}{{{S}_{MDH}}}=\frac{DP\sin \widehat{PDH}}{DM\sin \widehat{MDH}} \).
Mặt khác, áp dụng định lí sin cho \( \Delta ABC \):
\( \frac{DP}{DM}=\frac{\sin \widehat{DMP}}{\sin \widehat{DPM}}=\frac{\cos \widehat{{{O}_{1}}MN}}{\cos \widehat{{{O}_{2}}PQ}}=\frac{\sin \widehat{MNA}}{\sin \widehat{PQA}}=\frac{\sin \widehat{DNA}}{\sin \widehat{DQA}} \).
Áp dụng tiếp định lí sin cho \( \Delta DNA \) và \( \Delta DQA \), ta được:
\( \frac{PH}{MH}=\frac{\sin \widehat{DNA}\sin \widehat{PDH}}{\sin \widehat{DQA}\sin \widehat{MDH}}=\frac{\sin \widehat{DNA}}{\sin \widehat{MDH}}.\frac{\sin \widehat{PDH}}{\sin \widehat{DQA}} \)
\( =\frac{\sin \widehat{DNA}}{\sin \widehat{NDA}}.\frac{\sin \widehat{QDA}}{\sin \widehat{DQA}}=\frac{DA}{AN}.\frac{AQ}{DA}=\frac{AQ}{AN} \).
Kết hợp (1) \( \Rightarrow \frac{PH}{MH}=\frac{{{O}_{2}}A}{{{O}_{1}}A}\Rightarrow {{O}_{2}}P\parallel DH\parallel {{O}_{1}}M\Rightarrow DH\bot BC \).
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress









