Trung Tâm Luyện Thi Đại Học
Bài 12. Chuyển động ném
Khởi động trang 49
Nhảy xa là một ví dụ về chuyển động ném. Theo em, trong việc nhảy xa thì những yếu tố nào có tính quyết định đến thành tích nhảy của vận động viên?

Hướng dẫn giải:
Theo em, những yếu tố có tính quyết định đến thành tích nhảy của vận động viên là tốc độ chạy đà và góc giậm nhảy.
I. Chuyển động ném ngang – Trang 49, 50 & 51
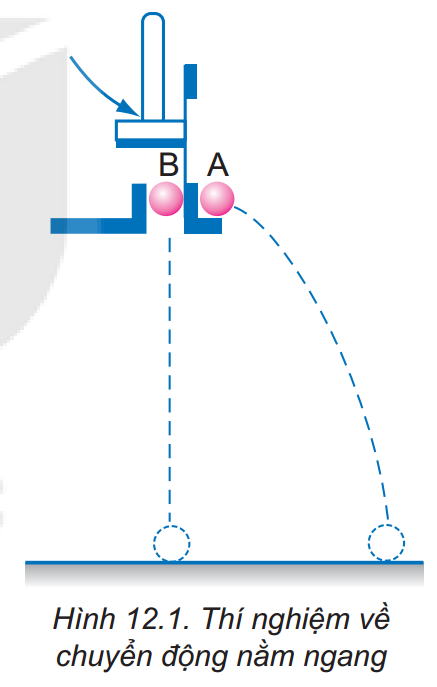
Hai viên bi có chạm đất cùng một lúc không?
Hướng dẫn giải:
Hai viên bi này chạm đất cùng lúc.
Hãy nhận xét về sự thay đổi vị trí theo phương thẳng đứng của hai viên bi sau những khoảng thời gian bằng nhau.

Hướng dẫn giải:
Sau những khoảng thời gian bằng nhau, ta thấy vị trí theo phương thẳng đứng của hai viên bi này là như nhau. Do đó, theo phương này hai viên bi chuyển động rơi tự do.
Hãy quan sát hình ảnh hoạt nghiệm ở Hình 12.2 để chứng tỏ chuyển động thành phần theo phương nằm ngang là chuyển động thẳng đều với vận tốc vx= v0.

Hướng dẫn giải:
Theo phương ngang, hình chiếu vị trí của viên bi A di chuyển được những quãng đường như nhau sau những khoảng thời gian bằng nhau. Do đó trên phương này, viên bi A chuyển động thẳng đều với vận tốc vx = v0.
1. Hãy đề xuất phương án thí nghiệm để kiểm tra những kết luận 1 và 2.
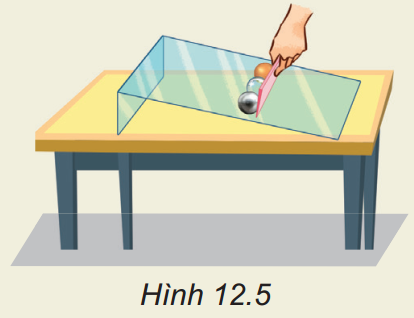
2. Dùng thước kẻ giữ ba viên bi (sắt, thủy tinh và gỗ) có cùng kích thước, trên một tấm thủy tinh đặt nghiêng trên mặt bàn rồi nâng thước lên (Hình 12.5). Hãy dự đoán tầm xa của ba viên bi và làm thí nghiệm kiểm tra.
Hướng dẫn giải:
1.
Kết luận 1: Tầm xa của vật bị ném ngang phụ thuộc vào độ cao H của vật khi bị ném và vận tốc ném. Nếu từ cùng một độ cao đồng thời ném các vật khác nhau với vận tốc khác nhau thì vật nào có vận tốc ném lớn hơn sẽ có tầm xa lớn hơn.
– Phương án thí nghiệm:
+ Dùng một cục tẩy chì và một nắp chai, đặt trên mép một mặt bàn nhẵn nằm ngang đặt cạnh một hố cát (mục đích để vật khi tiếp xúc với cát không bị nảy lên, đo tầm xa được chính xác hơn).
+ Lần lượt dùng tay búng vào cục tẩy và nắp chai các lực khác nhau sao cho lực búng vào cục tẩy mạnh hơn (cung cấp vận tốc đầu khác nhau).
+ Đo tầm xa của cục tẩy và nắp chai thì thấy cục tẩy có tầm xa lớn hơn.
\( \Rightarrow \)Tầm xa của vật bị ném ngang phụ thuộc vào độ cao H của vật khi bị ném và vận tốc ném. Nếu từ cùng một độ cao đồng thời ném các vật khác nhau với vận tốc khác nhau thì vật nào có vận tốc ném lớn hơn sẽ có tầm xa lớn hơn.
Kết luận 2: Nếu từ các độ cao khác nhau ném ngang các vật với cùng vận tốc thì vật nào được ném ở độ cao lớn hơn sẽ có tầm xa lớn hơn.
– Phương án thí nghiệm:
+ Dùng 2 cục tẩy giống nhau, hai chiếc bàn phẳng nhẵn có độ cao khác nhau (hai chiếc bàn đặt trên cùng một mặt phẳng nằm ngang), và một chiếc bút bi có nẫy bấm như hình dưới. Làm thí nghiệm cạnh một hố cát giống như thí nghiệm trên.
+ Đặt các cục tẩy trên các mặt bàn (đặt sát mép bàn).
+ Đặt bút bi sát với các cục tẩy và bấm nẫy để bút bi tác dụng lực vào cục tẩy làm cục tẩy chuyển động ngang.
+ Kết quả cục tẩy trên chiếc bàn có độ cao lớn hơn sẽ có tầm xa lớn hơn.
\( \Rightarrow \) Nếu từ các độ cao khác nhau ném ngang các vật với cùng vận tốc thì vật nào được ném ở độ cao lớn hơn sẽ có tầm xa lớn hơn.
2.
– Ba viên bi này có cùng độ cao H và có cùng vận tốc ban đầu nên tầm xa của ba viên bi này như nhau.
– Học sinh tự làm thí nghiệm kiểm tra.
Nếu đồng thời ném hai quả bóng giống nhau với những vận tốc bằng nhau theo phương nằm ngang từ hai độ cao h1, h2khác nhau (h1 < h2) thì:
a) Quả bóng ném ở độ cao nào chạm đất trước?
b) Quả bóng ném ở độ cao nào có tầm xa lớn hơn?
Hướng dẫn giải:
a) Ta có: \( t=\sqrt{\frac{2h}{g}}\Rightarrow \) t tỉ lệ thuận với \( \sqrt{h} \).
Vì \( {{h}_{1}}<{{h}_{2}} \) nên \( {{t}_{1}}<{{t}_{2}}\Rightarrow \) Quả bóng ném ở độ cao h1 chạm đất trước.
b) Ta có: \( L={{v}_{0}}\sqrt{\frac{2h}{g}}\Rightarrow L \) tỉ lệ thuận với \( \sqrt{h} \).
Vì \( {{h}_{1}}<{{h}_{2}} \) nên \( {{L}_{1}}<{{L}_{2}}\Rightarrow \) Quả bóng ném ở độ cao h2 có tầm xa lớn hơn.
Một máy bay chở hàng đang bay ngang ở độ cao 490 m với vận tốc 100 m/s thì thả một gói hàng cứu trợ xuống một làng đang bị lũ lụt. Lấy g = 9,8 m/s2và bỏ qua sức cản không khí.
a) Sau bao lâu thì gói hàng chạm đất?
b) Tầm xa của gói hàng là bao nhiêu?
c) Xác định vận tốc của gói hàng khi chạm đất.
Hướng dẫn giải:
Phân tích quá trình chuyển động ném ngang của vật.
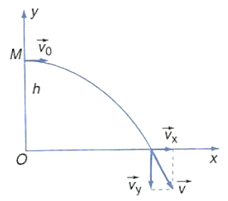
a) Gói hàng sẽ chạm đất sau khoảng thời gian t thỏa mãn:
\( h=\frac{1}{2}g{{t}^{2}}\Rightarrow t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2.490}{9,8}}=10\text{ }s \).
b) Tầm xa của gói hàng là:
\( L={{d}_{x\max }}={{v}_{0}}.t=100.10=1000\text{ }m \).
c) Khi chạm đất: \(v=\sqrt{v_{x}^{2}+v_{y}^{2}}\).
Thành phần chuyển động theo phương ngang: \( {{v}_{x}}={{v}_{0}}=100\text{ }m/s \).
Thành phần chuyển động theo phương thẳng đứng: \( {{v}_{y}}=g.t=\sqrt{2gh} \).
Vận tốc của gói hàng khi chạm đất là: \( v=\sqrt{2gh+v_{0}^{2}}=\sqrt{2.9,8.490+{{100}^{2}}}\simeq 140\text{ }m/s \).
II. Chuyển động ném xiên – Trang 51, 52, 53 & 54
Hãy tìm thêm ví dụ về chuyển động ném xiên trong đời sống.
Hướng dẫn giải:
Ví dụ:
– Chuyển động của quả bóng chuyền.

– Chuyển động của quả bóng rổ.

– Chuyển động của quả cầu.

Người ta bắn một viên bi với vận tốc ban đầu 4 m/s hướng lên theo phương xiên 45O so với phương nằm ngang. Coi sức cản của không khí là không đáng kể.
1. Tính vận tốc của viên bi theo phương nằm ngang và phương thẳng đứng tại các thời điểm: bắt đầu bắn, sau 0,1 s và sau 0,2 s.
2.
a) Viên bi đạt tầm cao H vào lúc nào?
b) Tính tầm cao H.
c) Gia tốc của viên bi ở tầm cao H có giá trị bằng bao nhiêu?
3.
a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí nào?
b) Viên bi có vận tốc cực tiểu vào thời điểm nào?
4.
a) Khi nào viên bi chạm sàn?
b) Xác định vận tốc của viên bi khi chạm sàn?
c) Xác định tầm xa L của viên bi.
Hướng dẫn giải:
1.
Chọn hệ trục tọa độ phân tích chuyển động ném xiên như hình dưới
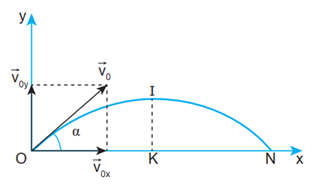
– Thời điểm bắt đầu bắn:
+ Vận tốc theo phương ngang: \( {{v}_{0x}}={{v}_{0}}\cos {{45}^{O}}=4.\frac{\sqrt{2}}{2}=2\sqrt{2}\text{ }m/s \).
+ Vận tốc theo phương thẳng đứng: \( {{v}_{0y}}={{v}_{0}}\sin {{45}^{O}}=4.\frac{\sqrt{2}}{2}=2\sqrt{2}\text{ }m/s \).
– Sau 0,1 s:
+ Vận tốc theo phương ngang: \( {{v}_{x}}={{v}_{0x}}=2\sqrt{2}\text{ }m/s \) (chuyển động thành phần theo phương ngang là chuyển động thẳng đều)
+ Vận tốc theo phương thẳng đứng: \( {{v}_{y}}={{v}_{0y}}-gt=2\sqrt{2}-9,8.0,1=1,85\text{ }m/s \).
– Sau 0,2 s:
+ Vận tốc theo phương ngang: \( {{v}_{x}}={{v}_{0x}}=2\sqrt{2}\text{ }m/s \) (chuyển động thành phần theo phương ngang là chuyển động thẳng đều)
+ Vận tốc theo phương thẳng đứng: \( {{v}_{y}}={{v}_{0y}}-gt=2\sqrt{2}-9,8.0,2=0,87\text{ }m/s \).
2.
a) Khi đạt tới tầm cao H thì:
\( {{v}_{y}}={{v}_{0y}}-gt=0\Rightarrow t=\frac{{{v}_{0y}}}{g}=\frac{2\sqrt{2}}{9,8}=0,289\text{ }s \).
b) Tầm cao H là: \( H=\frac{v_{0y}^{2}}{2g}=\frac{{{\left( 2\sqrt{2} \right)}^{2}}}{2.9,8}=0,408 \).
c) Gia tốc của viên bi ở tầm cao H: \( a=g=9,8\text{ }m/{{s}^{2}} \) vì khi vật đạt độ cao max vận tốc của vật bằng 0 và vật rơi xuống do chịu tác dụng của trọng lực.
3.
a) Vận tốc của viên bi có độ lớn cực tiểu ở vị trí tầm cao H = 0,408 m
b) Viên vi có vận tốc cực tiểu vào thời điểm vật bắt đầu chạm sàn vì khi đó vật bay ngược chiều dương đã chọn và vận tốc có giá trị âm:
\( {t}’=2t=2.0,289=0,578\text{ }s \).
4.
a) Khi viên bi chạm sàn thì thời gian chuyển động (gấp 2 lần thời gian từ lúc bắt đầu ném cho đến khi đạt tầm cao H) là: \( {t}’=2t=\frac{2{{v}_{0y}}}{g}=2.0,289=0,578\text{ }s \).
b) Khi chạm sàn: \( v=\sqrt{v_{x}^{2}+v_{y}^{2}} \).
Thành phần chuyển động theo phương ngang: \( {{v}_{x}}={{v}_{0x}}=2\sqrt{2}\text{ }m/s \).
Thành phần chuyển động theo phương thẳng đứng: \( {{v}_{y}}=\sqrt{2gh} \).
Suy ra: \( v=\sqrt{v_{0x}^{2}+2gh}=\sqrt{{{\left( 2\sqrt{2} \right)}^{2}}+2.9,8.0,408}\simeq 4\text{ }m/s \).
c) Tầm xa: \( L={{d}_{x\max }}={{v}_{0c}}.{t}’=2\sqrt{2}.0,578=1,635\text{ }m \).
1. Sử dụng được các công thức của chuyển động ném ngang để giải thích cách thả hàng cứu trợ bằng máy bay.
2. Vận dụng được kiến thức về chuyển động ném xiên để giải thích một số tình huống đơn giản trong cuộc sống. Ví dụ thành tích nhảy xa của vận động viên phụ thuộc vào góc nhảy, việc điều chỉnh góc bắn để có tầm đạn bay xa nhất của các pháo thủ.
Hướng dẫn giải:
1.
– Khi máy bay đang chuyển động theo phương ngang với vận tốc v0, người ta thả một thùng hàng xuống thì lúc đó thùng hàng sẽ chuyển động theo quán tính với vận tốc đúng bằng vận tốc máy bay đang chuyển động. Khi đó thùng hàng coi như một chuyển động ném ngang. Ngoài ra thùng hàng còn chịu ảnh hưởng của gió.
– Do đó, để những thùng hàng này có thể rơi đúng vị trí, người ta cần tính toán được vận tốc thả của thùng hàng khi bắt đầu thả (có thể là vận tốc tổng hợp của vận tốc máy bay khi đó và vận tốc gió), độ cao so với mặt đất để xác định được tầm xa của chúng theo công thức: \( L={{v}_{0}}\sqrt{\frac{2H}{g}} \).

Máy bay thả hàng cứu trợ
2.
– Chuyển động của vận động viên nhảy xa là chuyển động ném xiên. Do đó, thành tích của vận động viên cũng chính là tầm xa của vận động viên.
+ Tầm xa phụ thuộc vào góc theo công thức: \( L=\frac{v_{0}^{2}.\sin 2\alpha }{g} \).
+ Tầm xa lớn nhất khi \( \sin 2\alpha \) lớn nhất \( \Leftrightarrow \sin 2\alpha =1\Leftrightarrow \alpha ={{45}^{O}} \).
– Tương tự như trên, các pháo thủ điều chỉnh góc bắn \( \alpha ={{45}^{O}} \) thì sẽ có tầm đan bay xa nhất.
Hoạt động trải nghiệm trang 54
1. Tìm hiểu bằng lí thuyết
Vận dụng những kiến thức đã học về chuyển động ném để dự đoán về:
– Để ném ngang một vật đạt tầm bay xa lớn nhất thì phải chọn độ cao như thế nào?
– Để ném xiên một vật đạt tầm xa lớn nhất thì phải chọn góc ném như thế nào?
2. Lập phương án làm thí nghiệm để kiểm tra dự đoán.
3. Thực hiện thí nghiệm, rút ra kết luận.
4. Viết báo cáo về kết quả tìm được.
5. Trình bày báo cáo trước lớp.
Hướng dẫn giải:
1. Tìm hiểu bằng lí thuyết
– Để ném ngang một vật đạt tầm bay xa lớn nhất thì phải chọn độ cao lớn nhất.
– Để ném xiên một vật đạt tầm xa lớn nhất thì phải chọn góc ném
2. Lập phương án thí nghiệm
– Kiểm chứng kết quả ném ngang một vật đạt tầm bay xa lớn nhất thì phải chọn độ cao lớn nhất học sinh có thể tham khảo phương án thí nghiệm ở phần Hoạt động 1 trang 51 SGK Vật Lí 10.
– Kiểm chứng ném xiên một vật đạt tầm xa lớn nhất thì phải chọn góc ném ta sẽ sử dụng một mặt phẳng nghiêng có độ nghiêng thay đổi được (mục đích thay đổi góc nghiêng), dùng các một nam châm có gắn công tắc (giống như ở thí nghiệm kiểm chứng sự rơi tự do), viên bi sắt. Viên bi sắt được gắn vào nam châm, đặt ở khoảng giữa mặt phẳng nghiêng, bấm công tắc để viên bi bắn ra theo mặt phẳng nghiêng. Đo các kết quả tầm xa với các góc khác nhau
3. Học sinh tự viết ghi kết quả
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress

