Trung Tâm Luyện Thi Đại Học
Bài 8. Chuyển động biến đổi. Gia tốc
Khởi động trang 37
Hình dưới là ảnh chụp hoạt nghiệm thí nghiệm về sự thay đổi vận tốc của một ô tô đồ chơi chạy bằng pin có gắn anten dùng để điều khiển từ xa, trong ba giai đoạn chuyển động. Vận tốc trong ba giai đoạn chuyển động này có gì giống nhau, khác nhau?

Hướng dẫn giải:
Ảnh hoạt nghiệm cho biết hình ảnh chuyển động của vật trong những khoảng thời gian bằng nhau.
– Hình a: Trong cùng một khoảng thời gian, quãng đường ô tô chuyển động được tăng dần chứng tỏ vận tốc của xe tăng dần.
– Hình b: Trong cùng một khoảng thời gian, quãng đường ô tô chuyển động được như nhau chứng tỏ vận tốc của xe không thay đổi.
– Hình c: Trong cùng một khoảng thời gian, quãng đường ô tô chuyển động được giảm dần chứng tỏ vận tốc của xe giảm dần.
\( \Rightarrow \)Vận tốc trong 3 giai đoạn này giống nhau về phương và chiều, khác nhau về độ lớn.
I. Chuyển động biến đổi – Trang 37
Hãy tìm thêm ví dụ về chuyển động biến đổi trong cuộc sống.
Hướng dẫn giải:
– Chuyển động của xe đạp khi xuống dốc.

– Chuyển động của tàu khi sắp cập bến.

– Chuyển động của vận động viên điền kinh khi bắt đầu xuất phát.

II. Gia tốc của chuyển động biến đổi – Trang 38
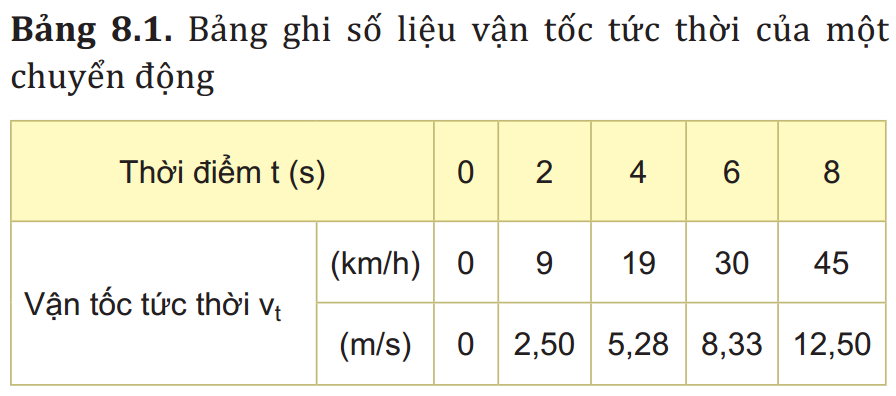
1. Xác định độ biến thiên vận tốc sau 8 s của chuyển động trên.
2. Xác định độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong 4 s đầu và trong 4 s cuối.
3. Các đại lượng xác định được ở câu 2 cho ta biết điều gì về sự thay đổi vận tốc của chuyển động trên?
Hướng dẫn giải:
1. Độ biến thiên vận tốc sau 8 s của chuyển động trên là:
\( \Delta v={{v}_{8}}-{{v}_{0}}=12,5-0=12,5\text{ }m/s \).
2.
– Độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong 4 s đầu là:
\( \frac{\Delta v}{\Delta t}=\frac{{{v}_{4}}-{{v}_{0}}}{4}=\frac{5,28-0}{4}=1,32\text{ }m/{{s}^{2}} \).
– Độ biến thiên của vận tốc sau mỗi giây của chuyển động trên trong 4 s cuối là:
\( \frac{\Delta v}{\Delta t}=\frac{{{v}_{8}}-{{v}_{4}}}{4}=\frac{12,5-5,28}{4}=1,805\text{ }m/{{s}^{2}} \).
3. Các đại lượng xác định được ở câu 2 cho ta biết sự thay đổi nhanh hay chậm của vận tốc.
Hãy chứng tỏ khi \( \vec{a} \)cùng chiều với \( \vec{v}\text{ }(a.v>0) \) thì chuyển động là nhanh dần, khi \( \vec{a} \) ngược chiều với \( \vec{v}\text{ }(a.v<0) \) thì chuyển động là chậm dần.
Hướng dẫn giải:
Ta có biểu thức tính gia tốc: \( a=\frac{\Delta v}{\Delta t}=\frac{{{v}_{t}}-{{v}_{0}}}{t-{{t}_{0}}} \).
– Chọn chiều dương là chiều chuyển động của vật.
– Giả sử vật chuyển động theo chiều dương nên \( v>0 \).
– Khi vật chuyển động nhanh dần thì vận tốc của vật cũng tăng dần, nên theo biểu thức tính gia tốc thì \( \Delta v>0\Rightarrow a>0\Rightarrow a.v>0 \).
– Khi vật chuyển động chậm dần thì vận tốc giảm dần nên \( \Delta v<0\Rightarrow a<0\Rightarrow a.v<0 \).
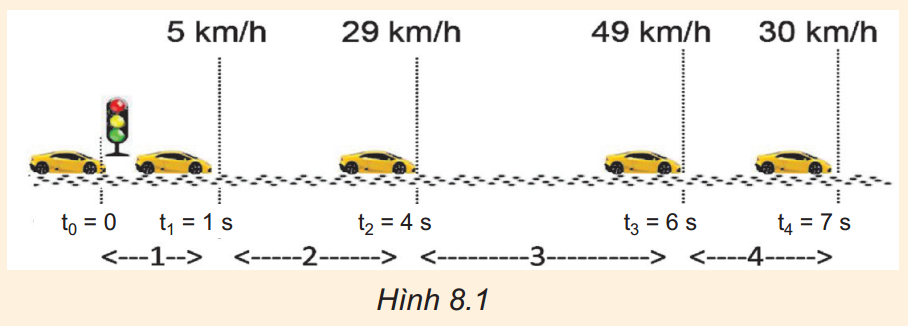
1.
a) Tính gia tốc của ô tô trên 4 đoạn đường trong Hình 8.1.
b) Gia tốc của ô tô trên đoạn đường 4 có gì đặc biệt so với sự thay đổi vận tốc trên các đoạn đường khác nhau?
2. Một con báo đang chạy với vận tốc 30 m/s thì chuyển động chậm dần khi tới gần một con suối. Trong 3 giây, vận tốc của nó giảm còn 9 m/s. Tính gia tốc của con báo.
3. Đồ thị ở Hình 8.2 mô tả sự thay đổi vận tốc theo thời gian trong chuyển động của một ô tô thể thao đang chạy thử về phía Bắc.
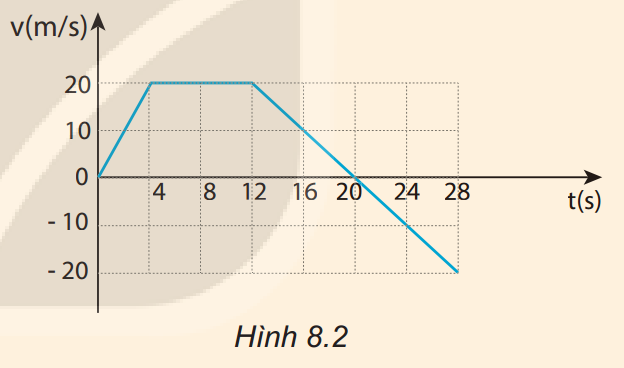
Tính gia tốc của ô tô:
a) Trong 4 s đầu.
b) Từ giây thứ 4 đến giây thứ 12.
c) Từ giây thứ 12 đến giây thứ 20.
d) Từ giây thứ 20 đến giây thứ 28.
Hướng dẫn giải:
1.
a) Đổi 5 km/h 1,39 m/s; 29 km/h 8,06 m/s;
49 km/h 13,61 m/s; 30 km/h 8,33 m/s
– Gia tốc của ô tô trên đoạn đường 1 là: \( {{a}_{1}}=\frac{\Delta {{v}_{1}}}{\Delta {{t}_{1}}}=\frac{1,39-0}{1-0}=1,39\text{ }m/{{s}^{2}} \).
– Gia tốc của ô tô trên đoạn đường 2 là: \( {{a}_{2}}=\frac{\Delta {{v}_{2}}}{\Delta {{t}_{2}}}=\frac{8,06-1,39}{4-1}\approx 2,22\text{ }m/{{s}^{2}} \).
– Gia tốc của ô tô trên đoạn đường 3 là: \( {{a}_{3}}=\frac{\Delta {{v}_{3}}}{\Delta t}=\frac{13,61-8,06}{6-4}\approx 2,78\text{ }m/{{s}^{2}} \).
– Gia tốc của ô tô trên đoạn đường 4 là: \( {{a}_{4}}=\frac{\Delta {{v}_{4}}}{\Delta {{t}_{4}}}=\frac{8,33-13,61}{7-6}=-5,28\text{ }m/{{s}^{2}} \).
b) Trên đoạn đường 1, 2, 3 thì gia tốc của xe dương vì vận tốc luôn tăng dần.
Trên đoạn đường 4 thì gia tốc âm vì vận tốc giảm dần.
2. Gia tốc của con báo là: \( a=\frac{\Delta v}{\Delta t}=\frac{9-30}{3}=-7\text{ }m/{{s}^{2}} \).
3.
a) Gia tốc của ô tô trong 4 giây đầu là: \( {{a}_{1}}=\frac{\Delta {{v}_{1}}}{\Delta {{t}_{1}}}=\frac{20-0}{4-0}=5\text{ }m/{{s}^{2}} \).
b) Gia tốc của ô tô từ giây thứ 4 đến giây thứ 12 là: \( {{a}_{2}}=\frac{\Delta {{v}_{2}}}{\Delta {{t}_{2}}}=\frac{20-20}{12-4}=0\text{ }m/{{s}^{2}} \).
c) Gia tốc của ô tô từ giây thứ 12 đến giây thứ 20 là: \( {{a}_{3}}=\frac{\Delta {{v}_{3}}}{\Delta {{t}_{3}}}=\frac{0-20}{20-12}=-2,5\text{ }m/{{s}^{2}} \).
d) Gia tốc của ô tô từ giây thứ 20 đến giây thứ 28 là: \( {{a}_{4}}=\frac{\Delta {{v}_{4}}}{\Delta {{t}_{4}}}=\frac{-20-0}{28-20}=-2,5\text{ }m/{{s}^{2}} \).
Dùng khái niệm gia tốc để giải thích một số hiện tượng về chuyển động dưới tác dụng của lực. Ví dụ như chuyển động rơi của một vật là chuyển động có gia tốc vì vật rơi chịu tác dụng của lực hút Trái Đất.
Hướng dẫn giải:
Ví dụ:
– Chuyển động của xe ô tô khi bắt đầu di chuyển là chuyển động có gia tốc vì ô tô chịu tác dụng của lực kéo của động cơ.

Giải thích: khi xe chịu tác dụng của lực kéo của động cơ, xe tăng tốc dần từ 0 cho đến một giá trị nào đó, vận tốc thay đổi trong một khoảng thời gian nên chuyển động này là chuyển động có gia tốc chịu tác dụng của lực.
– Chuyển động của xe máy khi chuẩn bị dừng đèn đỏ là chuyển động có gia tốc vì xe chịu tác dụng của lực ma sát.

Giải thích: khi xe chuẩn bị dừng đèn đỏ thì chịu tác dụng của lực ma sát ở đĩa phanh, lực này làm cho xe chuyển động chậm dần tức là vận tốc giảm dần trong một khoảng thời gian, chứng tỏ chuyển động này là chuyển động có gia tốc.
Các bài toán cùng chủ đề!
Các sách luyện thi do Trung tâm phát hành!
Trung Tâm Luyện Thi Đại Học được xây dựng trên WordPress

